位相におけるこれら5つの定義はなかなか理解が難しい。
そこでこの5つの概念の判断が容易になるための私なりのポイントをまずおさえる。
それは、「定義するときはイメージして、判断するときは機械的に」ということだ。
今回は定義をイメージしながら、考えていく。
閉集合
\((X,\mathcal{O})\)を位相空間とする。
補集合が開集合である部分集合を閉集合とよぶ。
閉集合と言われれば、境界を全て含んでいるような集合で・・・とイメージするかもしれない。
しかし、今の段階では境界という概念は位相には出てきていない。
もちろん今後境界という概念も位相に持ち込むのだが、そのときに閉集合という概念を用いて定義するため、閉集合は先に定めておかなければならない。
さて私たちの位相の手持ちを確認すると、「全体集合、位相、開集合」の3つだ。
これで、閉集合という概念を定義する必要がある。
そこで、イメージすることがポイントとなってくる。
「数直線でも座標平面でも、閉集合について今持っている手持ちの3つで表せる特徴は何か。」
とイメージする。
そうした上で閉集合の定義をもう一度見直すと、納得していただけると思う。
内部
\((X,\mathcal{O})\)を位相空間とする。
部分集合\(A \subset X\)について
\(A\)の内部とは、\(A\)に含まれる最大の開集合のこと。(記号:\(A^{。}\))
これは一つ例をイメージする。
例えば、図形と方程式の分野で円の内部と言われたら、どこを塗りつぶすだろうか。
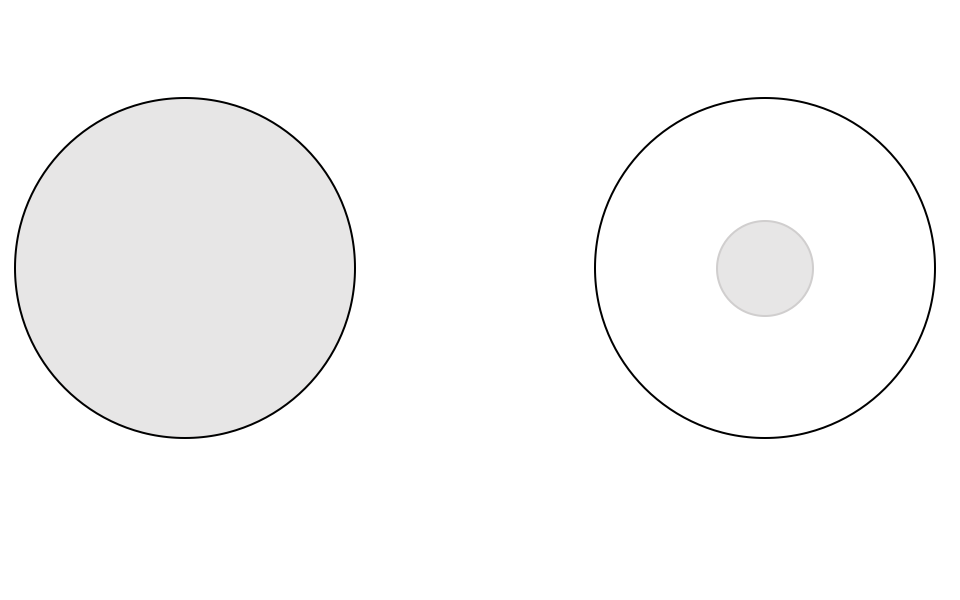
おそらく図形と方程式を習った人なら、右のような細胞核のようなものではなく
左をイメージすると思われる。
このことから、内部の定義の「最大の」と付けたくなる気持ちはわかるだろう。
また、今回の手持ちは「全体集合、位相、開集合、閉集合」の4つだ。
この中で内部として選ぶのなら、開集合になるのは想像できるだろう。
外部
\((X,\mathcal{O})\)を位相空間とする。
部分集合\(A \subset X\)について
\(A\)の外部とは、\(X-A\)の内部のこと。(記号:\(A^{e}\))
先ほどと同様に円の外部といったら円の内部と境界以外全てを塗りつぶすだろう。
外部は内部と対の概念で、集合と補集合という対の概念でうまく定義していることがわかる。
境界
\((X,\mathcal{O})\)を位相空間とする。
部分集合\(A \subset X\)について
\(A\)の境界とは、\(X-A^{。} \cup A^{e}\)のこと。(記号:\(A^{f}\))
日本語にすると、境界とは全体集合から内部と外部を取り除いたものということである。
普通、境界があって初めて内部と外部が生まれるような気がするのだが、
今までのでき方からわかるように位相は使える概念が少ないところからスタートしているため、
内部→外部→境界という順に定義している。
閉包
\((X,\mathcal{O})\)を位相空間とする。
部分集合\(A \subset X\)について
\(A\)の閉包とは、\(A\)を含む最小の閉集合のこと。(記号:\(A^{-}\))
注意してもらいたいのは、内部はAに含まれるのに対し、閉包はAを含むことだ。
包含関係は図のようになる。
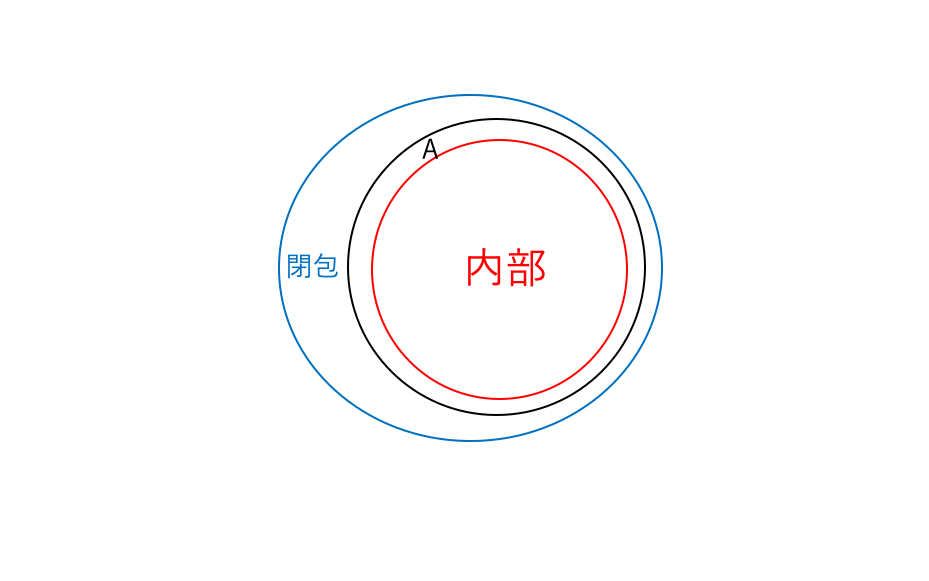
閉包といったらAを保護するために最小限のオブラートをつけるようなイメージだと思ってもらえればいい。
おまけ
今回は「定義するときはイメージして、判断するときは機械的に」の
「定義するときはイメージして」の部分をやった。
次回は「判断するときは機械的に」の部分をやっていく。



コメント