あらすじ
前回書いた、位相におけるこれら5つの概念を押さえるためのポイントをもう一度書く。
「定義するときはイメージして、判断するときは機械的に」ということだ。
前回は5つの概念をイメージしながら定義を確認した。(前回のリンクはこちら)
今回は1問問題を通して5つの概念について「判断するときは機械的に」ということを体験する。
問題
全体集合\(X=\{桃太郎,爺,婆,鬼 \}\)とし、
Xの位相を\(\mathcal{O}=\{ \emptyset ,X, \{桃太郎\},\{爺,婆\},\{桃太郎,爺,婆\} \}\)と定める。
(1)閉集合を全て求めよ。
(2)\(A=\{桃太郎,鬼\}\)とする。Aの内部、外部、境界、閉包を求めよ。
(1)閉集合
(1)閉集合の定義をおさらいする。(詳しくはこちら)
\((X,\mathcal{O})\)を位相空間とする。
補集合が開集合である部分集合を閉集合とよぶ。
このことから、一つ一つの開集合の補集合を見ていけば良い。
さて、位相の要素は開集合であるから、全ての開集合は以下の5つとなる。
\( \emptyset ,X, \{桃太郎\},\{爺,婆\},\{桃太郎,爺,婆\} \)
この補集合をそれぞれとると、以下のようになる。
\( X,\emptyset ,\{爺,婆,鬼\},\{桃太郎,鬼\},\{鬼\}\)
この対応関係をまとめておくと以下のようになる。
開集合:\( \emptyset ,X, \{桃太郎\},\{爺,婆\},\{桃太郎,爺,婆\} \)
閉集合:\( X,\emptyset ,\{爺,婆,鬼\},\{桃太郎,鬼\},\{鬼\}\)
(2)\(A=\{桃太郎,鬼\}\)とする。Aの内部、外部、境界、閉包を求めよ。
さて、ここから機械的にやっていく。
まずは、内部から定義を確認して解いていく。
内部
\((X,\mathcal{O})\)を位相空間とする。
部分集合\(A \subset X\)について
\(A\)の内部とは、\(A\)に含まれる最大の開集合のこと。(記号:\(A^{。}\))
内部は開集合であるから5つの選択クイズになる。
開集合:\( \emptyset ,X, \{桃太郎\},\{爺,婆\},\{桃太郎,爺,婆\} \)
閉集合:\( X,\emptyset ,\{爺,婆,鬼\},\{桃太郎,鬼\},\{鬼\}\)
また、\(A\)に含まれるという部分を読めば、\(A=\{桃太郎,鬼\}\)であるから、
\( \emptyset , \{桃太郎\}\)の2択にまで絞れる。
最後を決めるのが、最大性だ。\( \emptyset \subset \{桃太郎\}\)という関係が成り立つので、
Aの内部は\( \{桃太郎\}\)だとわかる。
「内部のイメージはこのようで…」と一切考えずに、定義にのみ従い機械的に判断する。
外部
\((X,\mathcal{O})\)を位相空間とする。
部分集合\(A \subset X\)について
\(A\)の外部とは、\(X-A\)の内部のこと。(記号:\(A^{e}\))
外部は内部を持って定義し、内部の選択肢は開集合であるから、今回も最初は5択クイズとなる。
開集合:\( \emptyset ,X, \{桃太郎\},\{爺,婆\},\{桃太郎,爺,婆\} \)
閉集合:\( X,\emptyset ,\{爺,婆,鬼\},\{桃太郎,鬼\},\{鬼\}\)
また、\(X-A=X-\{桃太郎,鬼\}=\{爺,婆\}\)であり、内部の定義よりそれに含まれるから、
\( \emptyset , \{爺,婆\}\)の2択にまで絞れる。
最後に、\( \emptyset \subset \{爺,婆\}\)という関係が成り立つので、最大性より
\(X-A\)の内部は\( \{爺,婆\}\)となる。
よってAの外部は\( \{爺,婆\}\)となる。
境界
\((X,\mathcal{O})\)を位相空間とする。
部分集合\(A \subset X\)について
\(A\)の境界とは、\(X-A^{。} \cup A^{e}\)のこと。(記号:\(A^{f}\))
境界はXからAの内部とAの外部を引いたものだ。
今回Aの内部は\( \{桃太郎\}\)で、外部は\( \{爺,婆\}\)なので、境界は
\(A^{f}=X-A^{。} \cup A^{e}=\{桃太郎,爺,婆,鬼 \} – \{桃太郎\} \cup \{爺,婆\}=\{鬼\}\)となることから、境界は\(\{鬼\}\)となる。
閉包
\((X,\mathcal{O})\)を位相空間とする。
部分集合\(A \subset X\)について
\(A\)の閉包とは、\(A\)を含む最小の閉集合のこと。(記号:\(A^{-}\))
閉包は閉集合であるから5択にまで絞れる。
開集合:\( \emptyset ,X, \{桃太郎\},\{爺,婆\},\{桃太郎,爺,婆\} \)
閉集合:\( X,\emptyset ,\{爺,婆,鬼\},\{桃太郎,鬼\},\{鬼\}\)
また、閉包は\(A\)を含むという部分を読めば、\(A=\{桃太郎,鬼\}\)であるから、
\( X , \{桃太郎,鬼\}\)の2択にまで絞れる。
最後を決めるのが、最小性だ。\( X \subset \{桃太郎,鬼\}\)という関係が成り立つので、
Aの閉包は\( \{桃太郎,鬼\}\)だとわかる。
おまけ
図は時折、人を間違った方向に導くことが多々ある。
今回の問題についてベン図を書くと、以下のようになる。
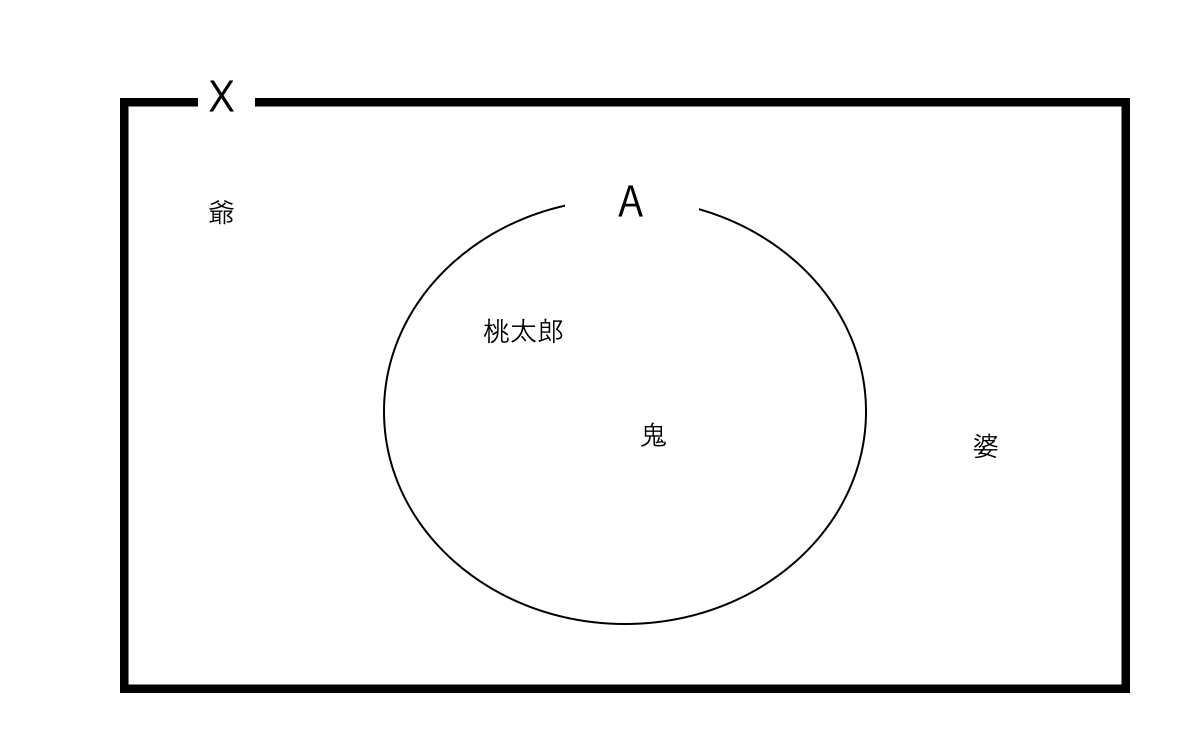
これを見てしまうと「内部は\( \{桃太郎,鬼\}\)で・・・」みたいな間違った考えを持ってしまう。
少なくともこの図を見て「境界は鬼だ!」とは想像つかないだろう。
だからイメージなどはなから持とうとせず、定義に従い、機械的にすることがオススメである。



コメント