あらすじ
実数ではなく複素数である数を虚数という。
「虚構」「虚言」など虚という字には実態が伴わないなどという意味がある。
また虚数は英語に直してもimaginary numberと表され、想像上のものとして扱われる。
では、虚数という概念は実数とは違って存在しないものなのだろうか?
今回はこの問いに対して、視覚的に話を始め、直観的に結論を出してみようと試みる。
自然数から有理数まで
まずは自然数(全体と0を含む集合)についてだ。
自然数(全体と0を含む集合)は下のように0を出発点としてポツポツポツ…と続いていく。
これは隙間がある状態である。これでは上の赤い部分を測ることができない。
そこで生まれるのが分数(正の有理数)や小数である。
こうすることによって間を埋めることができた。(視覚的には)
有理数から負の数へ
ここまでで「おや?」と思われた方もいるかもしれない。
中学校の頃から慣れ親しんでいた数直線は決して半直線をイメージして書かれたものではなかった。
そこで生み出されるのが、負の数という概念である。
ここで小学生では犯してはいけなかったタブーの一つ「1-3」について
答えることができるようになる。
これによって数直線を(視覚的に)描くことができたように思える。
しかしながらこれ以降の考え方が非常に重要になる。
有理数から実数へ
有理数は異なる2点をとってきたら必ずその間に有理数が存在する。(有理数の稠密性)
その性質もあり、有理数をプロットしていったものは一見数直線のように思える。
この記事でも視覚的にというところをカッコして示してきた。
しかしながら数直線にはまだまだ足りない要素がはるかに多くある。
数直線に対応しているのは有理数ではなく、実数なのだ。
ここを詳しくいうと有理数は加算無限個だが、実数は加算無限ではない。
(詳しくは濃度 有理数の濃度 実数の濃度)
この違いを視覚的に表現すると有理数は以下のような操作を無限回繰り返すことで得られる。
しかしながら実数は加算無限ではないのでこのような操作を無限回繰り返したところで
一生到達できない無限の世界である。
そのため先生が「数直線というのは点の集合なんだよ。」といってこの動作で板書したら
「先生、数直線が点の集合だというのは賛成ですが、
その動作では加算無限にしか到達しないので実数には対応しません。」
と言い返すことができる。(詳しくは抽象幾何)
これは人間の目には見えない世界になるので、いくら見ようとしても違いはわかりはしない。
(bump of chickenの天体観測みたいなもの。)
ではこの違いをどうやって視覚的に見分ければ良いのだろうか?
それはざっくりいうと「1点を基準に引きちぎってみる。」と見分けることができる。
試しに有理数と実数の違いを\(\sqrt{2}\)を基準に引きちぎってみる。
そうすると有理数は以下のようになる。
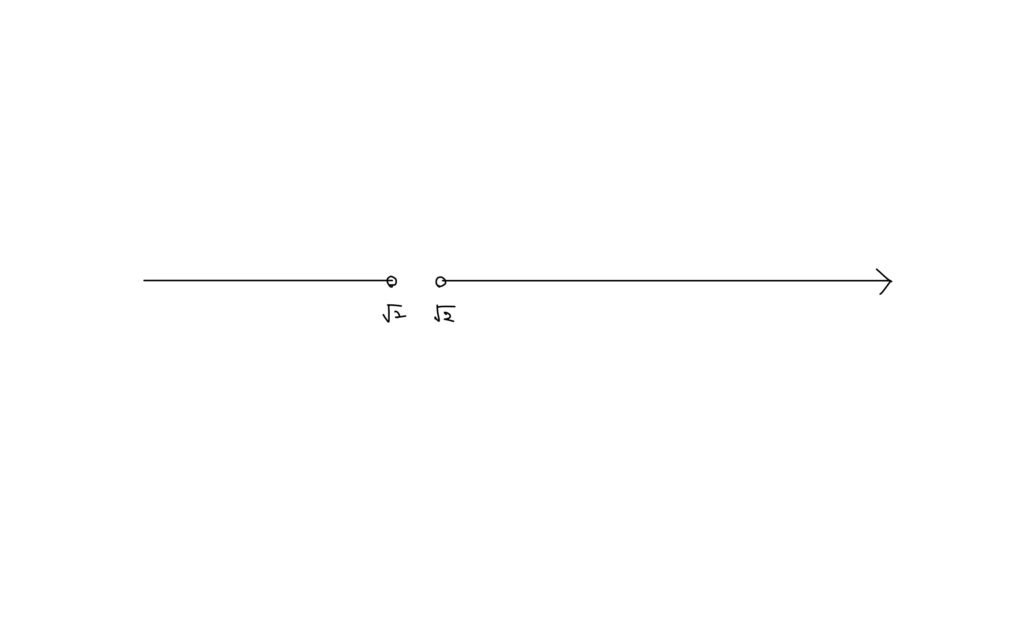
それに対して実数は以下の2パターンのどちらかになる。
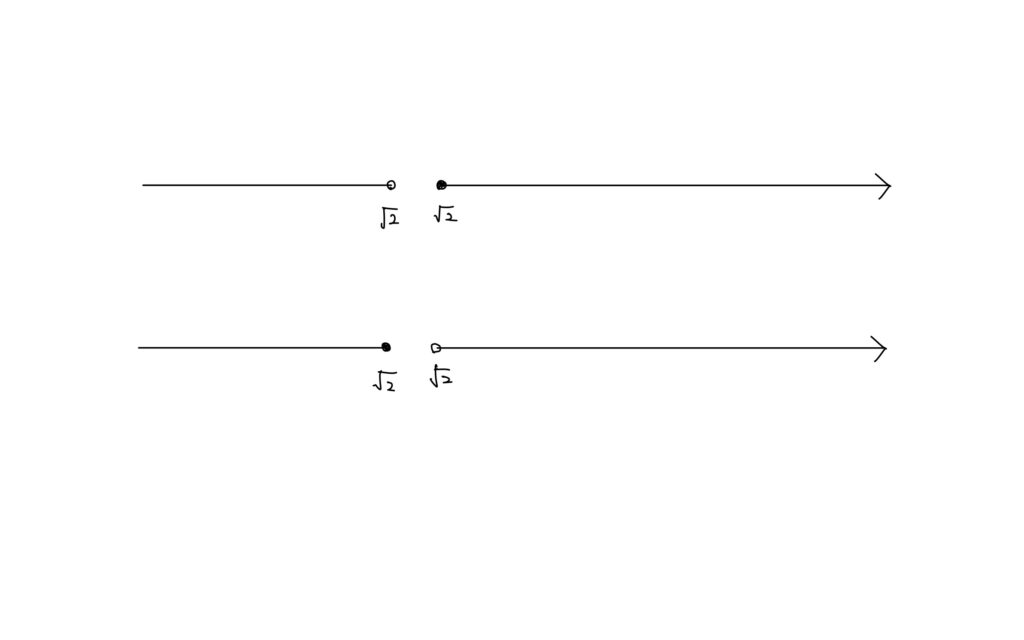
このように有理数では\(\sqrt{2}\)で分けると最大値や最小値がどちらにもできないが、
実数では\(\sqrt{2}\)で分けると最大値か最小値がどちらかに必ずできる。
今回は\(\sqrt{2}\)で分けたが、
実数は任意の点で分けたとき、最大値か最小値がどちらかに必ずできる。(実数の連続性)
いよいよ複素数へ
まず自然数から始まり、視覚的に認識できる「間」を埋めるために正の有理数を付け加えた。
そして負の数を付け加えることで半直線(ぽいもの)から直線(ぽいもの)へと進化した。
実数を付け加えると一見変化したようには思えない。
しかしながら1点を基準に分けてみると有理数とは違うことが視覚的にも明らかになった。
ここで、いよいよ複素数になると視覚的には何が起こるのかを見ていく。
実は考え方は負の数を付け加えたときと似ていて、直線から進化するのだ。
それが、直線から平面に進化する。このように複素数を平面にして表したものを複素数平面という。
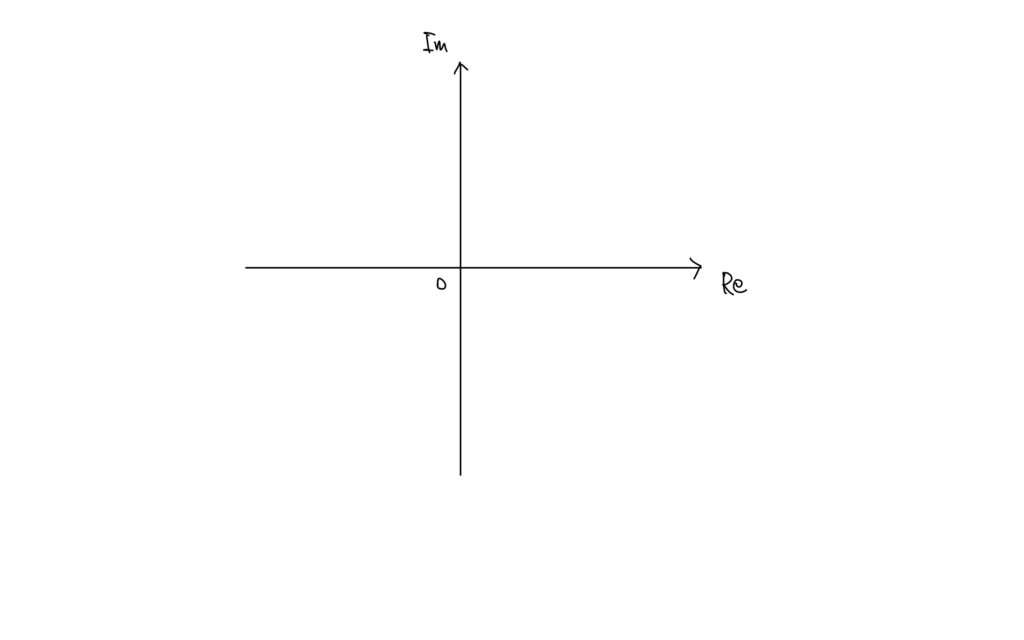
ここで今まで当たり前と思っていた大小関係、順序関係という数の概念がぶっ壊される。
この子どもの頃からの当たり前が覆されるので複素数は受け入れづらいのかもしれない。
終わりに
複素数というの受け入れづらい内容第一位だと思っている。
(これは完全に主観です。)
そんな中、学校ではその感覚は無視されてどんどん進められていく。
しかしながら歴史をみるとアルキメデスでも負の数が解になることを誤りだと考えたり、
ピタゴラスでも無理数を否定している。
このことを踏まえると、複素数は今の時代だからこそ学習内容となっているものだとわかる。
なんなら複素数を最初に発見したとされるカルダノも
「数ではないけど、とりあえず認めてから話を進めよっか。」というノリで持ち出している。
このことから複素数も受け入れられない人でも
「受け入れられるかどうかは微妙だけどとりあえず学んでみるか」
というノリを持ってみるのはいかがだろうか。

コメント