はじめに
前回は、実数と濃度が等しい集合たちについて考察した。
そこの証明の際に使ったのがベルンシュタインの定理である。
今回はそのベルンシュタインの定理について証明していく。
ベルンシュタインの定理
集合\(X,Y,Z\)について\(X \subset Y \subset Z\)が成り立っているとする
このとき\(X\)と\(Z\)の濃度が等しいならば,\(Y\)の濃度も等しい.

いやいやいやいや、当たり前じゃね??
そう思われるかもしれない。
例えば直感では、自然数と有理数が濃度が等しかったら整数も等しくなってほしいだろう。
しかしながら濃度は集合の包含関係ではなく、全単射の存在で定義している。
そのため、全単射が存在するかに全てが関わっているため、この定理は全く自明ではない。
この証明はあるアイデアで突破されるのだが、なかなか議論が長い。
そのため、イラストなどを用いながら証明を進めていく。
ベルンシュタインの定理の証明
集合\(X,Y,Z\)について\(X \subset Y \subset Z\)が成り立っているとする
このとき\(X\)と\(Z\)の濃度が等しいならば,\(Y\)の濃度も等しい.
(証明)
\(|X|=|Z|\)より\(Z\)から\(X\)への全単射\(f\)が存在する。
ここで\(Z\)を\(X=A,Y-X=B,Z-Y=C\)と3つの部分集合に分割する。
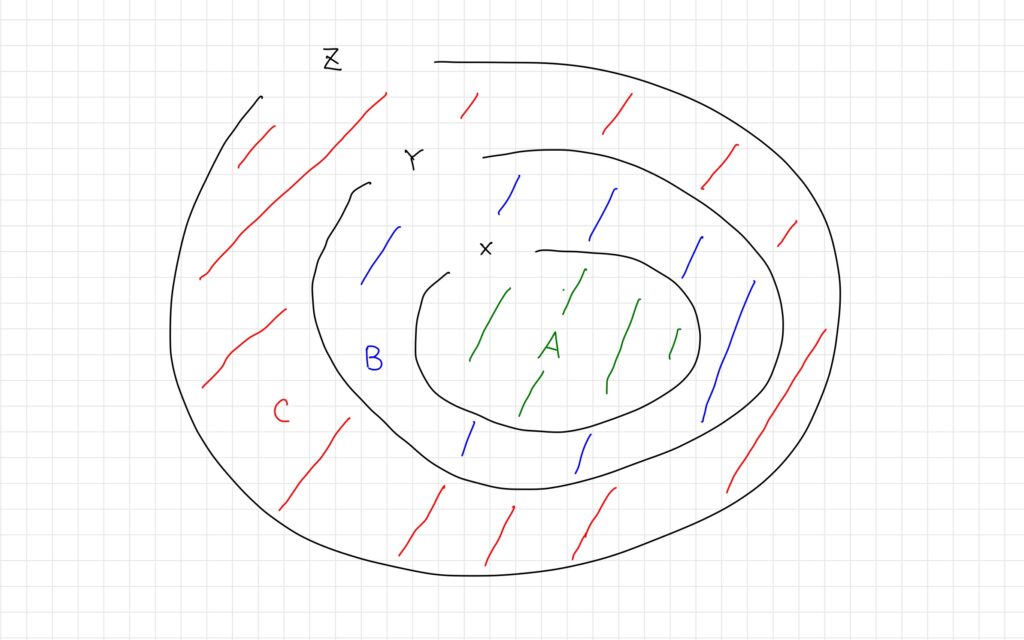
このとき\(X=A,Y=A\cup B,Z=A\cup B\cup C\)で表せる。
\(A_1=f(A),B_1=f(B),C_1=f(C)\)とおくと、\(f\)は全単射だから
\(|A|=|A_1|,|B|=|B_1|,|C|=|C_1|\)が成り立つ。
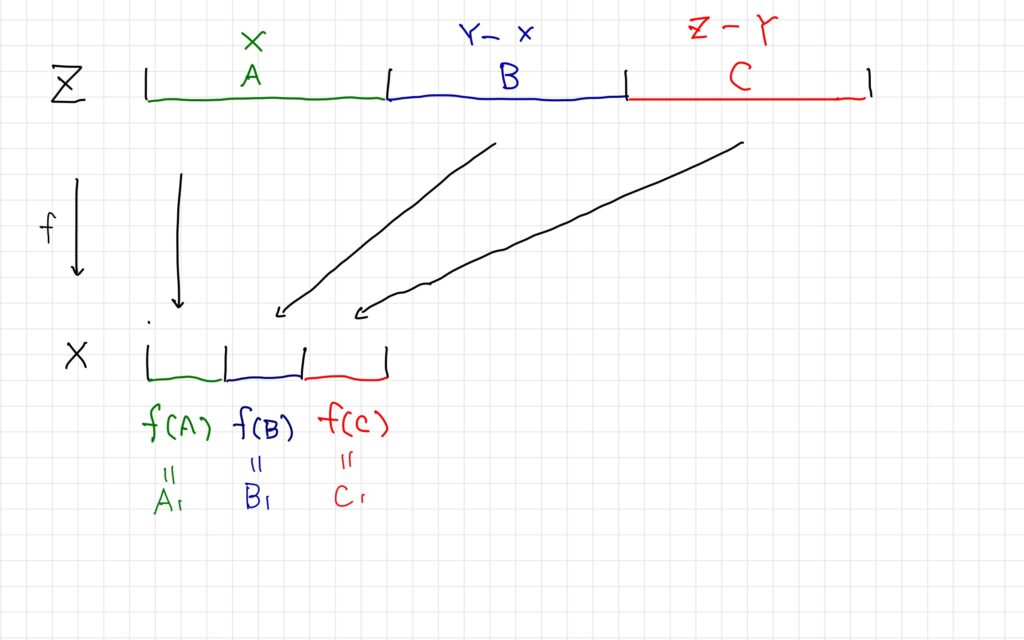
これを帰納的に繰り返し\(A_{n+1}=f(A_n),B_{n+1}=f(B_n),C_{n+1}=f(C_n)\)とする。
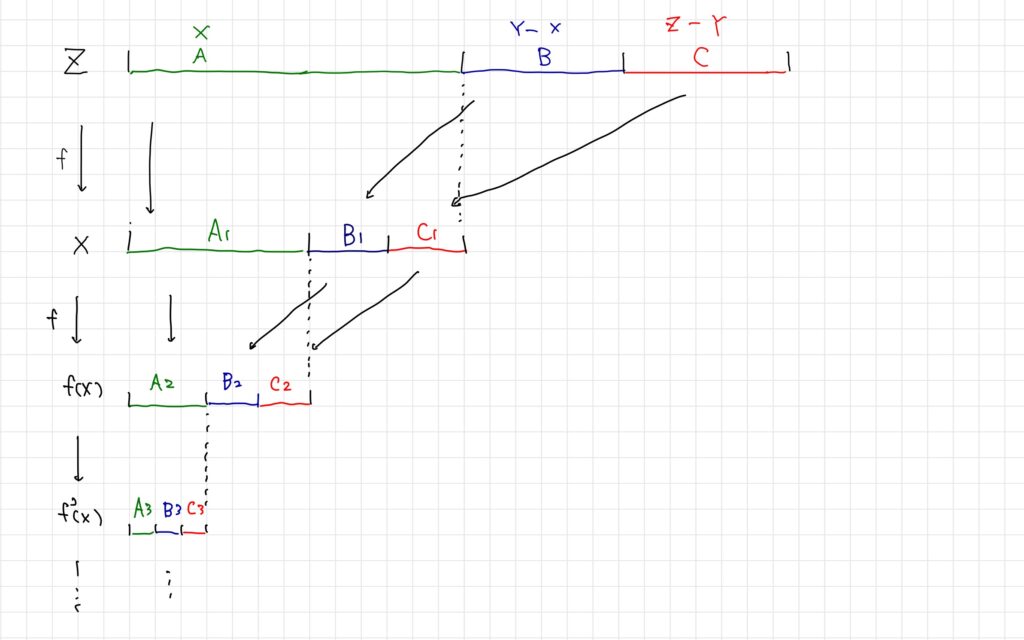
特に着目していただきたいのは、以下の2つだ。
・\(f\)の全単射性から\(|A_n|=|A_{n+1}|,|B_n|=|B_{n+1}|,|C_n|=|C_{n+1}|\)となる。
・\(f:Z\rightarrow X\)は全射だから\(A_{n+1}=A_n\cup B_n\cup C_n\)となる。
この2点を踏まえると、\(Z=A\cup B\cup C=A_1\cup B_1\cup C_1\cup B\cup C\)
\(=A_2\cup B_2\cup C_2\cup B_1\cup C_1\cup B\cup C\) \(=A_3\cup B_3\cup C_3\cup B_2\cup C_2\cup B_1\cup C_1\cup B\cup C\) \(=A_4\cup B_4\cup C_4\cup B_3\cup C_3\cup B_2\cup C_2\cup B_1\cup C_1\cup B\cup C\) \(\cdots\)となっていく。
ここで\(D=\cap \{A_n|n\in \mathbb{N}\}\)とおくと、先程の等式は以下のようになる。
\(Z=D\cup B\cup C \cup B_1 \cup C_1\cup B_2\cup C_2 \cup B_3\cup C_3 \cdots \cup B_n \cup C_n \cdots \)同じように\(Y\)についてもこのように考えると、
\(Y=A\cup B=A_1\cup B_1\cup C_1 \cup B\) \(Y=D\cup B \cup B_1 \cup C_1\cup B_2\cup C_2 \cup B_3\cup C_3 \cdots \cup B_n \cup C_n \cdots\)\(Y,Z\)の違いはどこかというと\(C\)があるかないかである。
ここでようやく舞台が整った。
早速全単射\(g:Z\rightarrow Y\)を作っていく。
証明の肝
先程、手に入れた事実をもう一度確認する。
・\(f\)の全単射性から\(|A_n|=|A_{n+1}|,|B_n|=|B_{n+1}|,|C_n|=|C_{n+1}|\)となる。
・\(Z=D\cup B\cup C \cup B_1 \cup C_1\cup B_2\cup C_2 \cup B_3\cup C_3 \cdots \cup B_n \cup C_n \cdots \)
・\(Y=D\cup B \cup B_1 \cup C_1\cup B_2\cup C_2 \cup B_3\cup C_3 \cdots \cup B_n \cup C_n \cdots\)
・\(Z\)と\(Y\)の違いは\(C\)があるかないか
この4点をもとにして,全単射\(g:Z\rightarrow Y\)を作っていく。
まず、\(D\)についてはそのまま\(D\)に送れば良い。
次に、\(B,B_1,B_2,B_3,\cdots\)についてもそのまま\(B,B_1,B_2,B_3,\cdots\)に送れば良い。
問題は\(C,C_1,C_2,C_3,\cdots\)と\(C_1,C_2,C_3,\cdots\)をどう繋ぐかだ。
ここで、一番最初にあげたポイント
・\(f\)の全単射性から\(|A_n|=|A_{n+1}|,|B_n|=|B_{n+1}|,|C_n|=|C_{n+1}|\)となる。
について特に\(|C_n|=|C_{n+1}|\)を使う。
さて、\(f\)は全単射だったことを思い出すと、\(|C|=|C_1|\)であり、\(f\)で送れば、\(C\)と\(C_1\)を全単射で繋ぐことができる。
次に各\(n \in \mathbb{N}\)について、\(|C_n|=|C_{n+1}|\)であるから\(C_n\)と\(C_{n+1}\)の間に全単射が存在する。
よって、\(C,C_1,C_2,C_3,\cdots\)と\(C_1,C_2,C_3,\cdots\)は1個ずらしで繋げば良いとわかる。
これによって全単射が構成された。きちんと書くと、
(i)\(x\in C\cup C_1\cup C_2\cup C_3 \cup \cdots\)のとき\(\hspace{3mm}g(x)=f(x)\)
(ii)(i)以外のとき(\(x\in D\cup B\cup B_1\cup B_2\cup B_3\cup \cdots\)のとき)\(\hspace{3mm}g(x)=x\)
と\(g:Z\rightarrow Y\)を定めれば、\(g\)は全単射となる。
よって\(Z\)と[latexY][/latex]の間に全単射が存在したので、\(|Z|=|Y|\)
終わりに
ベルンシュタインの定理はアイデア1つで突破できている。
しかしながらその構成方法が厄介なため解読するのに時間がかかる。
図を用いながら説明したものが理解の手助けになっていれば幸いだ。
\(\)
コメント