位相における連続の定義
位相における連続の定義は以下のようであった。(詳しくは位相における連続)
\((X,\mathcal{O}_X),(Y,\mathcal{O}_Y)\)をどちらも位相空間とする。
写像\(f:X \rightarrow Y\)が連続であるとは、以下の条件を満たすこと。
\(^{\forall}O_Y \in \mathcal{O}_Y\)について\(^{\exists}O_X \in \mathcal{O}_X \hspace{2mm}s.t.\hspace{2mm}f^{-1}(O_Y)=O_X\)
では、位相における連続はなぜこのような定義になっているのだろうか。
それは距離空間における連続の同値命題が由来する。
今回はそもそも距離空間における連続の定義はなんだったかを確認する。
距離空間における連続の定義
\((X,d_X),(Y,d_Y)\)をどちらも距離空間とする。
写像\(f:X \rightarrow Y\)が連続であるとは、以下の条件を満たすこと。
\(^{\forall} x \in X ,\)\(^{\forall} \epsilon >0\)について\(\hspace{2mm} ^{\exists} \delta >0\)\(\hspace{2mm}s.t.\hspace{2mm} f(B(x,\delta))\subset B(f(x),\epsilon)\)
これは、「任意に\(x\)を\(X\)からとってくる。そして、\(f(x)\)について任意に\(\epsilon\)近傍を考える。
これに対しxについて上手い具合に\(\delta\)近傍をとると、fで送ると先ほどの\(\epsilon\)近傍にすっぽり含まれる」
という意味だ。
文章でいってもわかりづらいので、図によってサポートしてもらう。
①任意に\(x\)を\(X\)からとってくる。
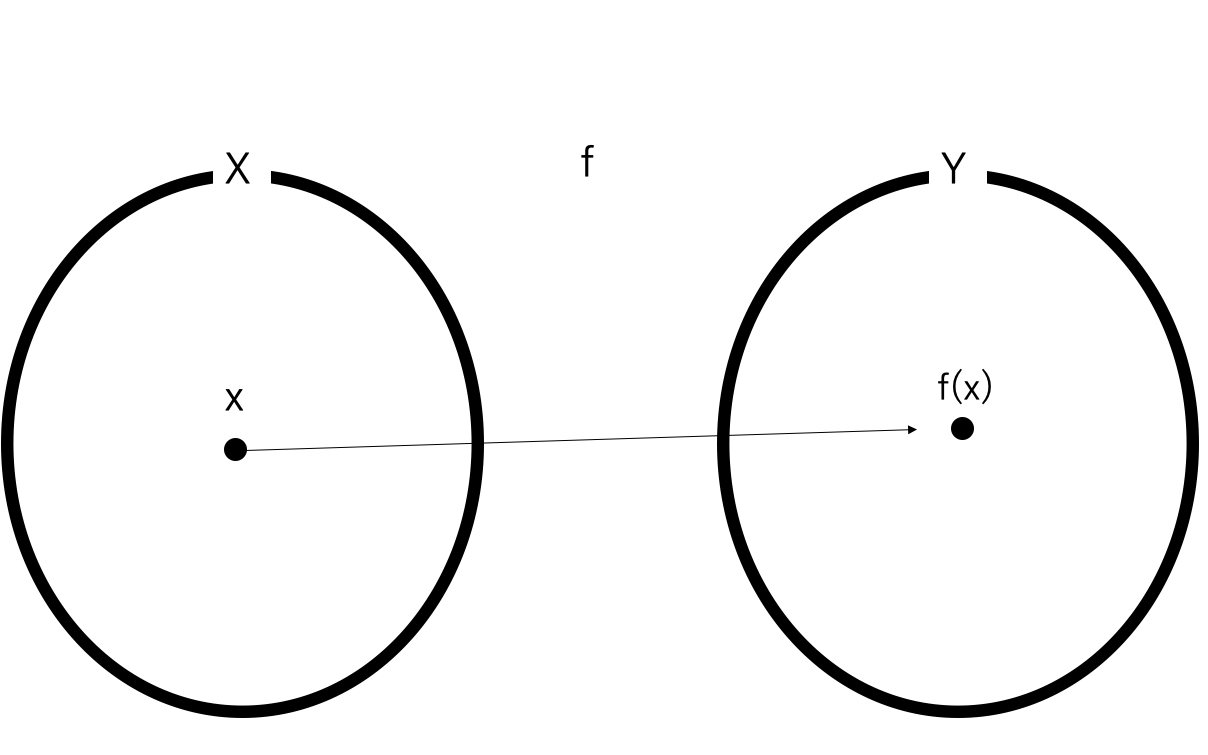
②\(f(x)\)について任意に\(\epsilon\)近傍を考える。
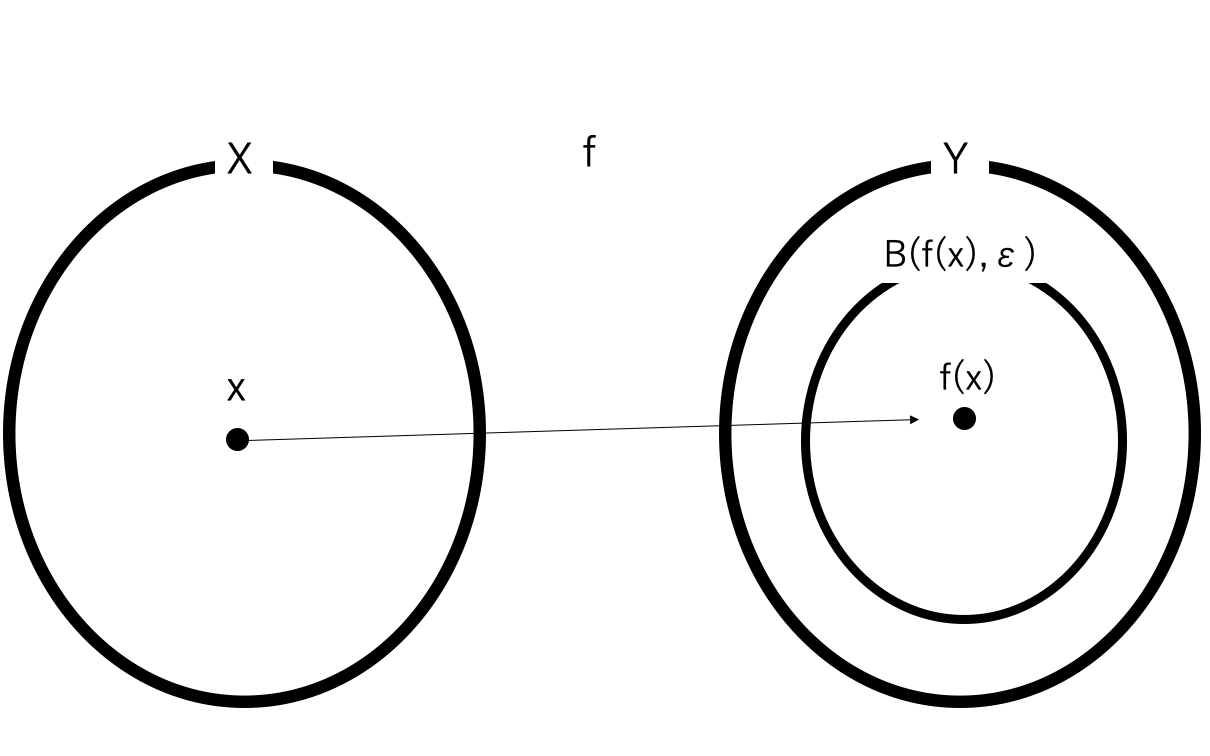
③xについて上手い具合に\(\delta\)近傍をとる。
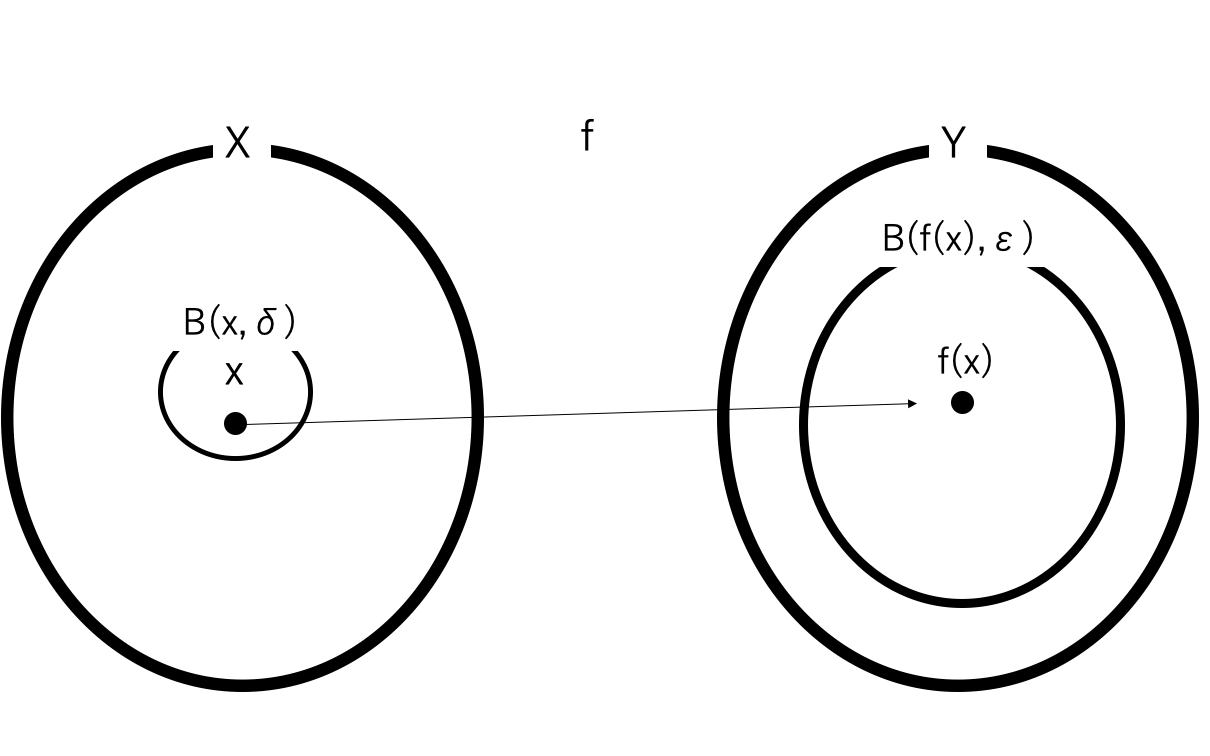
④\(\delta\)近傍をfで送ると、\(\epsilon\)近傍にすっぽり含まれる。
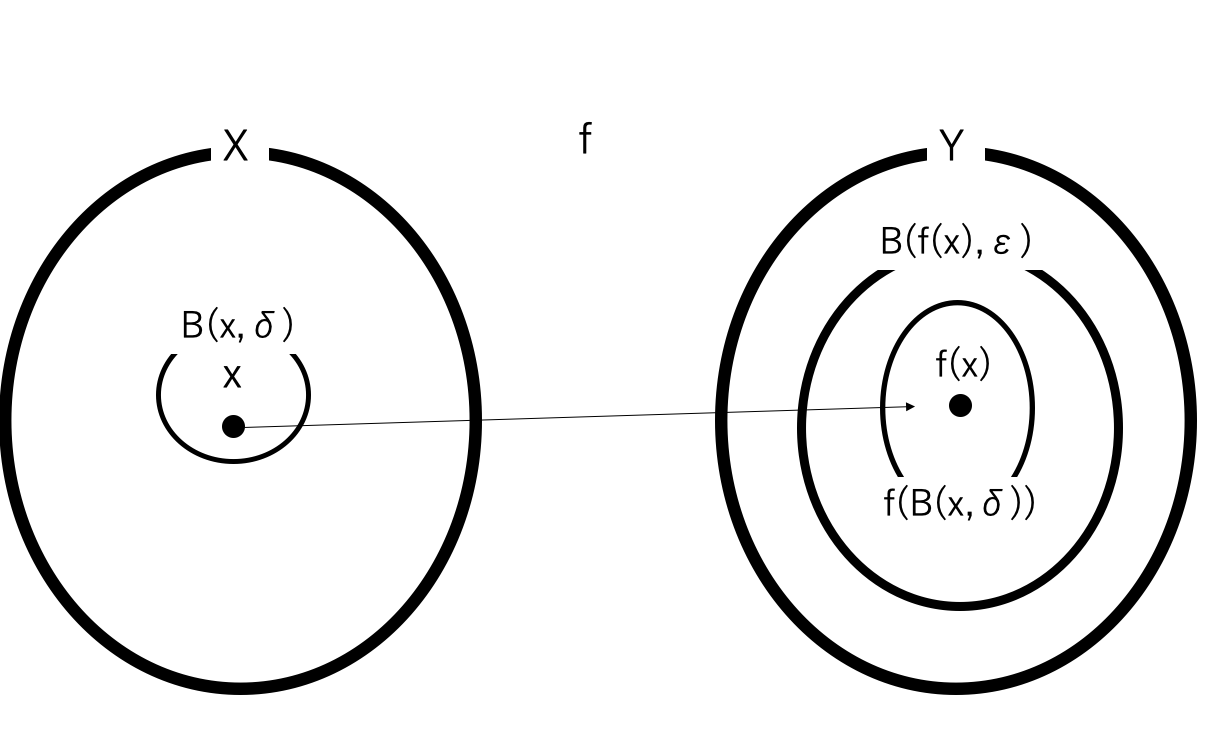
みたいなイメージだ。
これが距離空間における連続の定義だ。
おまけ
今回は距離空間における連続の定義を確認した。
次回はいよいよなぜ位相の定義はあのようなのかというところに迫る。



コメント