はじめに
基本群の定義は以下のようであった.(詳しくは基本群とは何か?)
\((X,\mathcal{O})\) を位相空間とする。
\(^{\forall}x_0 \in X\) について\(x_0\) の基本群\(\pi_1(X,x_0)\)とは
\(\pi_1(X,x_0):=\{ \alpha \mid \alpha はx_0 を基点とするループ\}/_{\simeq_p}\)のことである.
ざっくりいうと「ループを集めたもので,連続変形できるものは同じものとみなしましょう」
というものが基本群である.
この基本群についてどういった場面で使えるのかを説明する.
基本群のニュアンス
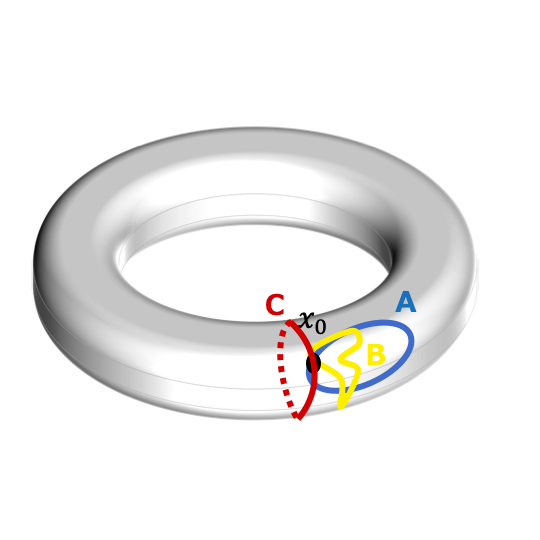
基本群では連続変形できるものは同じものとみなしましょうというルールがあった.
そのため上の図の\(A\) と\(B\) は一緒の元だった.
しかしながら\(C\) は連続変形できないので\(A\) とも\(B\) とも異なる元だった.
このように基本群というのは,感覚的には穴を調査することができるのだ.
例えば,次のようなループを考える.
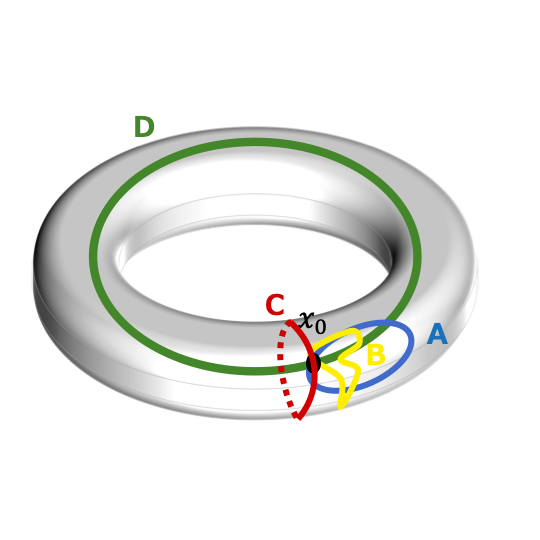
この\(D\) はまたまた連続変形できないので,違う元になる.
こちらも穴によって生まれる違いである.
この前提知識を蓄えた上で次の命題で基本群の意味を考える.
基本群の意味を教えてくれる命題
閉区間 \([0,1]\) はコンパクトだが,\(\mathbb{R}\) はコンパクトでないので同相でないという見極め方を以前に紹介した.
以下の定理では基本群でもそのようなことができるのではないかというアイデアだ.
基本群は位相不変量である.
この定理では「基本群が違ったら,位相は同相じゃない」ことを教えている.
例えば,円周\(S^1\) と閉区間\([0,1]\) はどちらもコンパクトである.
しかしながら感覚的には,「円周には穴があるけど,閉区間には穴ないじゃん」と言いたい.
そんな時に役立つのが基本群である.
\(S^1\) の基本群は\(\mathbb{Z}\) と同型で\([0,1]\)の基本群は\(\{1\}\) と同型である.
このことから基本群が群同型でないため,\(S^1\)と\([0,1]\) は同相でないことがわかる.
このようにコンパクトでは見極めきれなかったものを見極めることができる.
終わりに
先程サラッと\(S^1\)は\(\mathbb{Z}\) と同型と言ったが,
証明するにはいくつかの準備が必要である.
一番のカギとなるのが,被覆空間というものである.
そもそも被覆空間とは何か?,被覆空間と基本群はどのようにつながっているのか?
基本群が位相不変量であることを示すのはどうやって示すのか?
など疑問が色々残るが,続々と解決していきたい.

コメント