はじめに
基本群の定義は以下のようなものであった.
(詳しくは基本群とは何か?)
\((X,\mathcal{O})\) を位相空間とする。
\(^{\forall}x_0 \in X\) について\(x_0\) の基本群\(\pi_1(X,x_0)\)とは
\(\pi_1(X,x_0):=\{ \alpha \mid \alpha はx_0 を基点とするループ\}/_{\simeq_p}\)のことである.
ざっくり言うと
「基本群の元はループ.ただし連続変形できるものは同じものとみなしましょう」
となる.
しかしながらこれがなぜ群になるのだろうか?
今回はこのことについて直観的に説明する.
基本群の演算
基本群の演算\(*\)はざっくり言うと「ループ同士を繋ぐ」と言うものだ.
ドーナツの例で確認する.
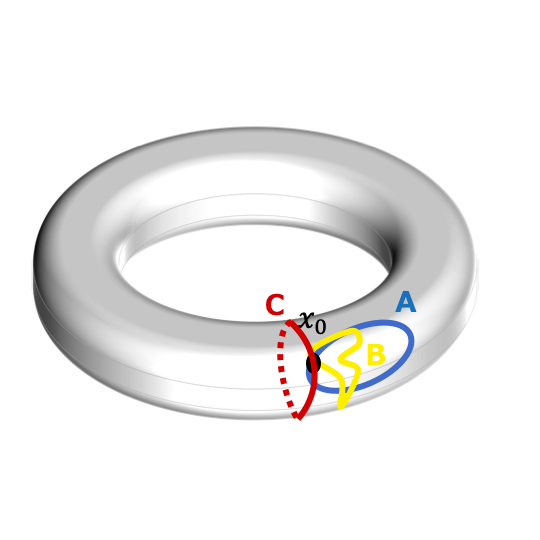
例えば,\(A*B\) は「\(A\)を通った後,\(B\)を通る」
という道だ.
これも\(x_0\) から始まって\(x_0\) に帰ってくるので,感覚的にループになることがわかる.
きちんと定義すると以下のようになる.
\((X,\mathcal{O})\) を位相空間とする。
\(^{\forall}x_0 \in X\) について\(\alpha,\beta\) を\(x_0\) を基点とするループとする.
\(\alpha,\beta\) の積\(\alpha *\beta\) とは
\(\alpha * \beta(t) = \left\{ \begin{array}{ll} \alpha(2t) & (0\leq t \leq \frac{1}{2})\\ \beta(2t-1) & (\frac{1}{2}\leq t \leq 1) \end{array} \right.\)と定義する.
ここで,「なんで\(\frac{1}{2}\) が出てくるの?」と言う疑問が生まれる.
これは,そもそも道が\([0,1]\rightarrow X\) という連続写像で定義域が\([0,1]\)なのがポイントだ.
ざっくり言うと「1秒間にどんな足跡を辿るのか」というのが道なので\(\alpha\) を通った後に\(\beta\) を通るなら,\(\alpha\) も\(\beta\) も半分の時間で通る必要がある.
このため,道の積はこのような定義になっている.
また「\(t=1\) のとき\(\alpha(1)\)にも\(\beta(0)\)にもなるけど大丈夫?」という不安がある.
これはどちらもループなので終点も始点も\(x_0\) であることを思い出すと一致していることがわかる.
それではなぜこれが群をなすのかを具体例を用いて直観的に説明する.
円周の基本群
円周のループを4つみていく.
まずは一周のループだ.
次にこのような元がある.
こちらは円周を2周するループだ.
1周する元と2周する元は連続変形できないので,これは基本群で異なる元である.
このようになにも動かないループもある.普段使っている「ループ」というニュアンスだと「本当にループか?」と思ってしまうが,これは数学上はループである.
これと道の積をとっても連続変形により元のループと一緒の元になる.
そのため,この元は基本群の単位元になっている.
最後の例はこれだ.
これは例1を逆まわりにした元である.
実はこの例1と例4の道の積は連続変形により単位元のループと等しくなる.
このことから例4は例1の逆元となる.
また,例2に対しては例2を逆再生した元が逆元となる.
このようにして\(S^1\)の基本群は本当に群になっている.
終わりに
今回の説明は直観的であったため,ふわふわした感覚を持った方もいるかもしれない.
一番の原因は連続変形という言葉をきちんと定義していないのだ.
この連続変形には道ホモトピーというものが必要になる.
次の回ではこの道ホモトピーについて定義する.


コメント