分度器幾何

あらすじ

今まで、抽象幾何、結合幾何、計量幾何、パッシュ幾何と制約を増やしていった。

今回は小学生の頃から習ってきた、角度を測るということが平面幾何的に初めて登場する。

定義

分度器幾何

パッシュ幾何\((\mathcal{P},\mathcal{L},d)\)に対して、

分度器関数\(m\)を1つ指定した時、組\((\mathcal{P},\mathcal{L},d,m)\)を分度器幾何という。

計量幾何以降の平面幾何はどのような平面上で\((\mathcal{P})\)どのような直線の取り方をし、\((\mathcal{L})\)
そして、どのように距離を測るか\((d)\)の3つにより定まっていた。

そのため、計量幾何を受け継いでいるパッシュ幾何も\((\mathcal{P},\mathcal{L},d)\)という組に対し、使う言葉だった。

「そこに分度器関数というものをさらに付け加えましょうね。」と宣言したのが、分度器幾何だ。

では、その分度器関数とはなんぞやということを下で解説する。

分度器関数のための事前準備

分度器関数を定める前にいくつか準備しておく。

まず測る対象として角というものを定義しなければならない。
そんなもの小学生の時から習っていると言いたくなるのだが、ここで聞かれているのは
「数学的に、平面幾何学的に角とは何だろうか。」ということだ。

しかし角を定義するにあたり、手持ちの材料を見てみると点と直線と距離関数のみだ。

そのため、2点を通る直線→半直線→角という順番に定義する。

2点を通る直線

異なる2点を通る直線と聞くと、一意に決まると勝手にイメージしてしまう。
しかしながら平面幾何学としては、このことが要求されているのは、結合幾何が初めてだ。
(詳しくは結合幾何)

そのため、今回はパッシュ幾何は前提条件としてあるので、
パッシュ幾何は結合幾何だということを思い出せば、2点を通る直線の一意性は使っても良い。

2点を通る直線

異なる2点\(P,Q\in \mathcal{P}\)を通る唯一の直線を\(\overleftrightarrow{PQ}\)と表記する。

半直線

半直線と聞くと、ある点をスタートして一方向に向かって永遠に伸び続けるイメージがある。
しかしながら平面幾何学として「永遠に伸び続ける」
すなわち直線に無数の点が含まれているのは計量幾何が初めてだ。
ましてや、方向などという概念はまだ出てきていない。

そこで、先ほどの一意性を使いながら、「間にある」ということを定義し、数学的に定義する。

間にある

共線的な3つの異なる点\(A,B,C\)を考える。

\(d(A,B)+d(B,C)=d(A,C)\)が成立する時、点\(B\)は点\(A\)と点\(C\)の間にあるという。

この時\(A-B-C\)と表す。

この間にあるという定義によってまず線分というものが定義できるようになった。

線分

異なる2点\(A,B\)に対し、

\(\overline{AB}=\{C\in \mathcal{P}|A-C-B\}\cup \{A,B\}\)をAからBまでの線分という。

この定義を見て鋭い人は「おや？」と思う人もいるかもしれない。「\(d(A,A)+d(A,B)=0+d(A,B)\)だから\(A,B\)自身も\(A,B\)の間にあるの点ではないか。」
しかしながら、「間にある」の定義の一番初めに共線的な3つの異なる点を対象としているため、
残念ながら\(A,B\)は\(A\)と\(B\)の間にあるとは言えない。

さて半直線を定義していくのだが、「間にあるという概念だけで半直線を定義できるのだろうか」と疑問に思うかもしれない。

しかしながらこの半直線の定義は見事に間にあるという概念だけで我々のイメージを表している。

半直線

異なる2点\(A,B\)に対し、

\(\overrightarrow{AB} =\overline{AB} \cup \{C\in \mathcal{P}|A-B-C\}\)を\(A\)から\(B\)への半直線という。

また点\(A\)を半直線\(\overrightarrow{AB}\)の始点という。

線分を超えたその先の点たちを「\(B\)が間にある」と捉え直すのが今回のミソだ。

初めて見たときは、私も思わずなるほど！と唸った。

角

いよいよ角を定義していく。だんだん分度器関数に近づいてきている。

角

\(A,B,C\)を共線的でない3点とする。

\(\angle ABC=\overrightarrow{BA}\cup \overrightarrow{BC}\)を角\(ABC\)という。

また、このとき、点\(B\)を角\(\angle ABC\)の頂点という。

つまり角とは、始点のみを共有する2つの半直線の和集合である。

そのため、半直線上の点のみを対象としていることがわかる。
次に角の内部を定義する。

角の内部というと角に挟まれている方と言いたくなるが、数学的には全く言い得ていない。
実は角の内部の定義には、半平面が必要なので、パッシュ幾何が重要になってくる。
(詳しくはパッシュ幾何)

角の内部

\(\angle ABC\)の内部\(int(\angle ABC)\)とは、
直線\(\overleftrightarrow{AB}\)の\(C\)を含む側の半平面と
直線\(\overleftrightarrow{BC}\)の\(A\)を含む側の半平面の共通部分とする。

理解を助ける図はこのような感じ。

直線\(\overleftrightarrow{AB}\)の\(C\)を含む側の半平面と

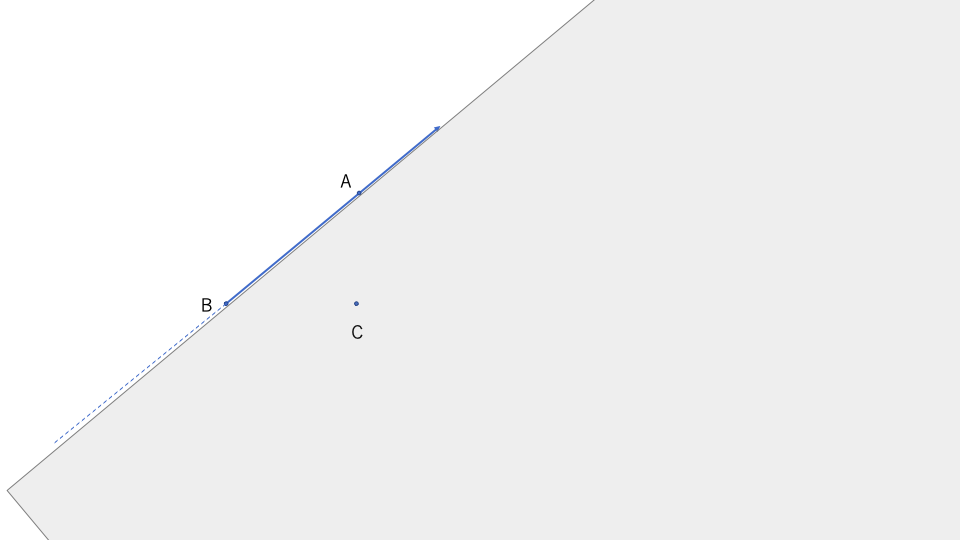
直線\(\overleftrightarrow{BC}\)の\(A\)を含む側の半平面の

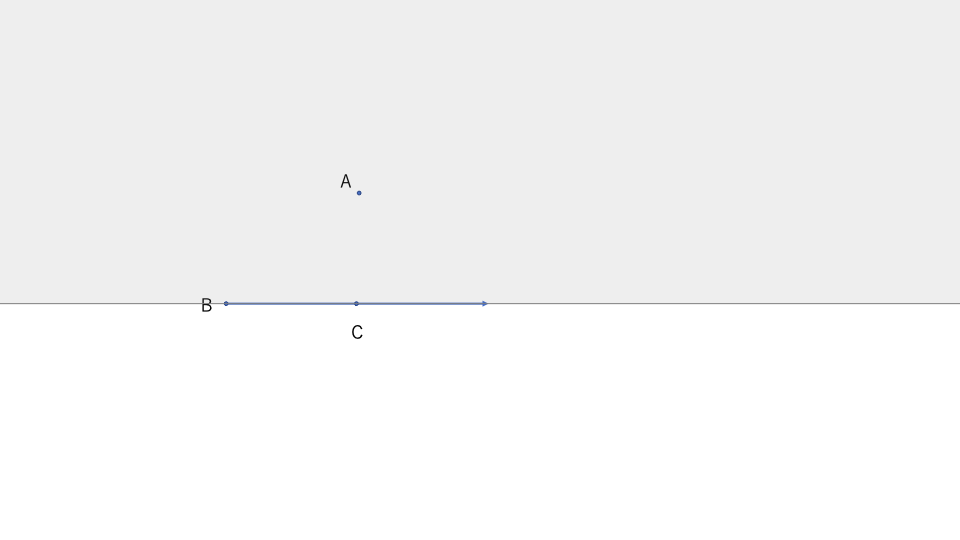
共通部分。

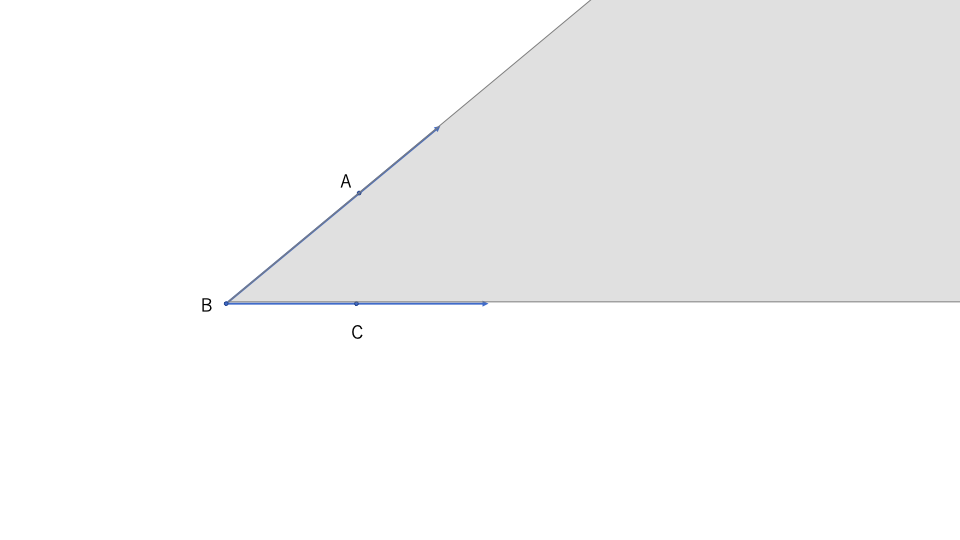
ようやく角とその内部を定義することができた。次はいよいよ分度器関数の定義だ。

分度器関数

パッシュ幾何\((\mathcal{P},\mathcal{L},d)\)における角全体の作る集合族を\(\mathcal{A}\)とする。

関数\(m:\mathcal{A}\rightarrow \mathbb{R}\)が次の3つの条件を満たすとき、分度器関数と呼ばれる。

\(1.\angle ABC \in \mathcal{A} \rightarrow 0<m(\angle ABC)<180\)

\(2.\overrightarrow{BC}\)の定める半平面\(H\)を考える。
\(\hspace{5mm}\)このとき\(^{\forall}\theta \in (0,180) \hspace{3mm}^{\exists _1}\overrightarrow{BA}\hspace{2mm}s.t.\hspace{2mm}m(\angle ABC)=\theta\)

\(3.D\in int(\angle ABC)\Rightarrow m(\angle ABD)+m(\angle DBC)=m(\angle ABC)\)

このとき、値\(m(\angle ABC)\)をその角の角度とよぶ。

1.では角度は0より大きい値かつ180より小さい値しか取らないと条件づけている。
「あれ、小学校の時に0°や240°とか習ったのになぁ。」と思う方もいらっしゃるかもしれない。

まず角度というのは出力結果が実数であるため、分度器関数的に°という単位がつくのはおかしい。さらに、現在角の定義で共線的でない3点であることを要求しているため、
前者は分度器関数としては受け付けない。
また、角度を関数で定義しているため、角に対してただ１つの値を決める必要がある。
そのため後者も分度器関数としては受け付けない。

2.では指定した角度を実現する角を半平面上にただ一つだけ作れることを条件づけている。
この時のただ一つとは、半直線がただ一つに定まるという意味である。
決して、点がただ一つに定まるといっていないところに注意が必要である。

3.では点\(D\)が\(\angle ABC\)の内部にあるとき、角度の足し算ができることを条件づけている。

これによって、分度器関数を定義することができた。