連続
\((X,\mathcal{O}_X),(Y,\mathcal{O}_Y)\)をどちらも位相空間とする。
写像\(f:X \rightarrow Y\)が連続であるとは、以下の条件を満たすこと。
\(^{\forall}O_Y \in \mathcal{O}_Y\)について\(^{\exists}O_X \in \mathcal{O}_X \hspace{2mm}s.t.\hspace{2mm}f^{-1}(O_Y)=O_X\)
定義解説
連続という概念を位相に持ち込むことが今回のテーマである。
早速一文目から見ていく。
\((X,\mathcal{O}_X),(Y,\mathcal{O}_Y)\)をどちらも位相空間とする。
連続という性質は写像に与えられるため、写像を考えるために二つの位相空間を用意する。
\(^{\forall}O_Y \in \mathcal{O}_Y\)について\(^{\exists}O_X \in \mathcal{O}_X \hspace{2mm}s.t.\hspace{2mm}f^{-1}(O_Y)=O_X\)
「Yという写像のゴール地点の空間からどんな開集合をfで戻しても、
それがXの開集合そのものになっている」ということをいっている。
図で表すと下図のようになる。
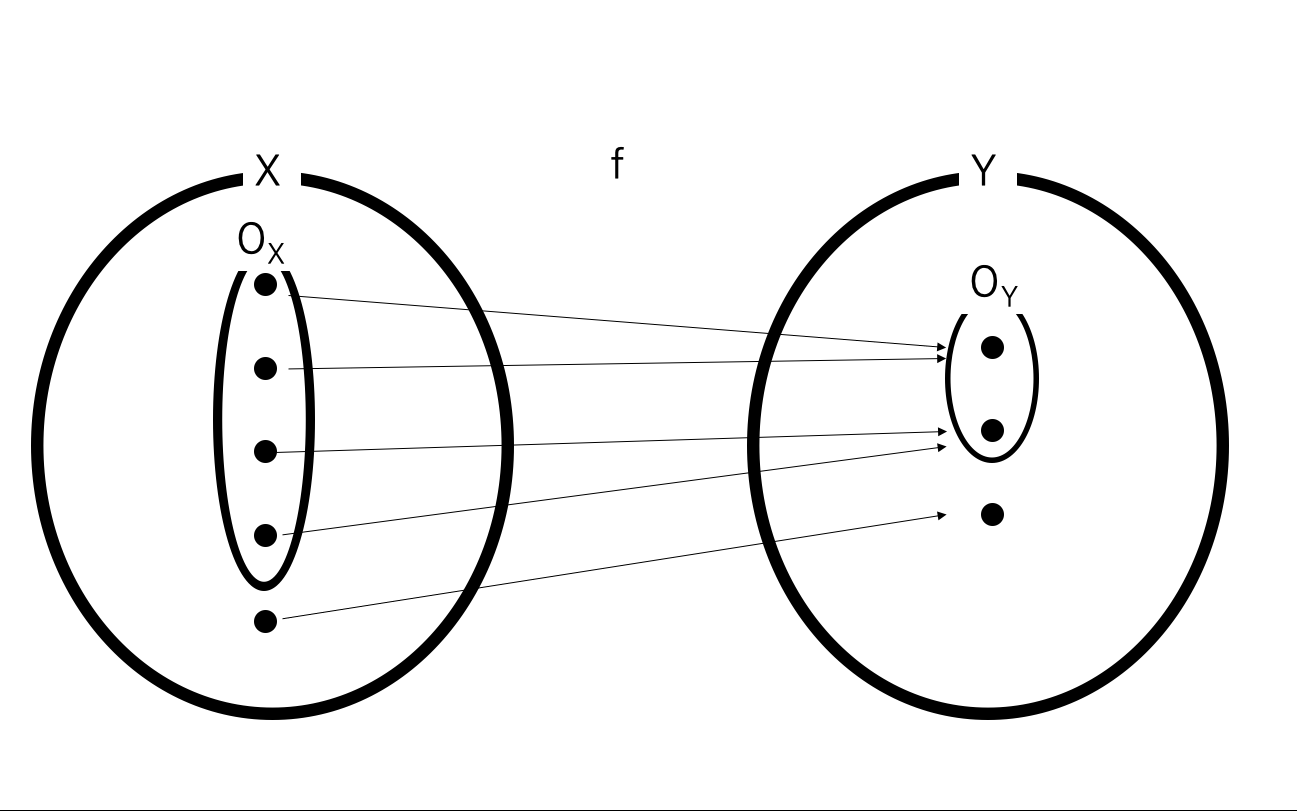
このアイデアはどこからきたのかは距離空間での連続性についての同値命題が鍵を握る。
次回はこの同値命題について書く。



コメント