sinを微分するとなぜcosなの？

はじめに

高校2年生の時に，三角関数と微分をそれぞれ習う．

微分と言ったら私が高校２年生の時には「なんか次数が下がって前出てくるやつ」
としか思ってなかった．

今回はそもそも微分とはなんだったかというところを振り返り，そのあと実際に
\(\sin x\)を微分してみる．

そうすると，困ったことに二つよくわからないものが出てくる．

それについて考えた後にもう一度\(\sin x \) の微分について考える．

そもそも微分とは？

高校生の間は，微分は「接線の傾きを求めるもの」と思ってほしい．

直線を書くにあたって必要な点は何点だろうか？

直線は2つ通る点があって初めて1本にバシッと決まる．

そして傾きはその2点のxとyの増加量を用いて求められる．

しかし残念なことに接点は1点しかない．

そこでわざと\(y=f(x)\) 上に2点目を作ってみるのだ．

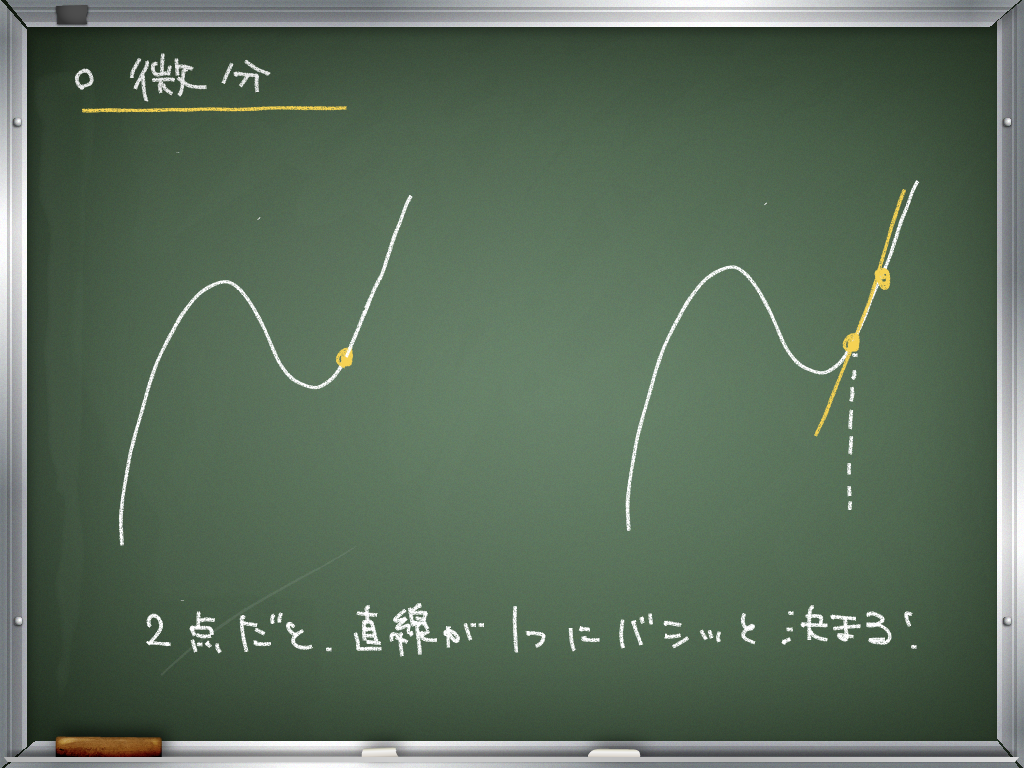
この直線を接線にするためには，このもう１つの点を限りなく近づけるという発想が必要になる．

そこで，「極限」という操作が必要になる．

このことを踏まえて微分の式を見てみる．

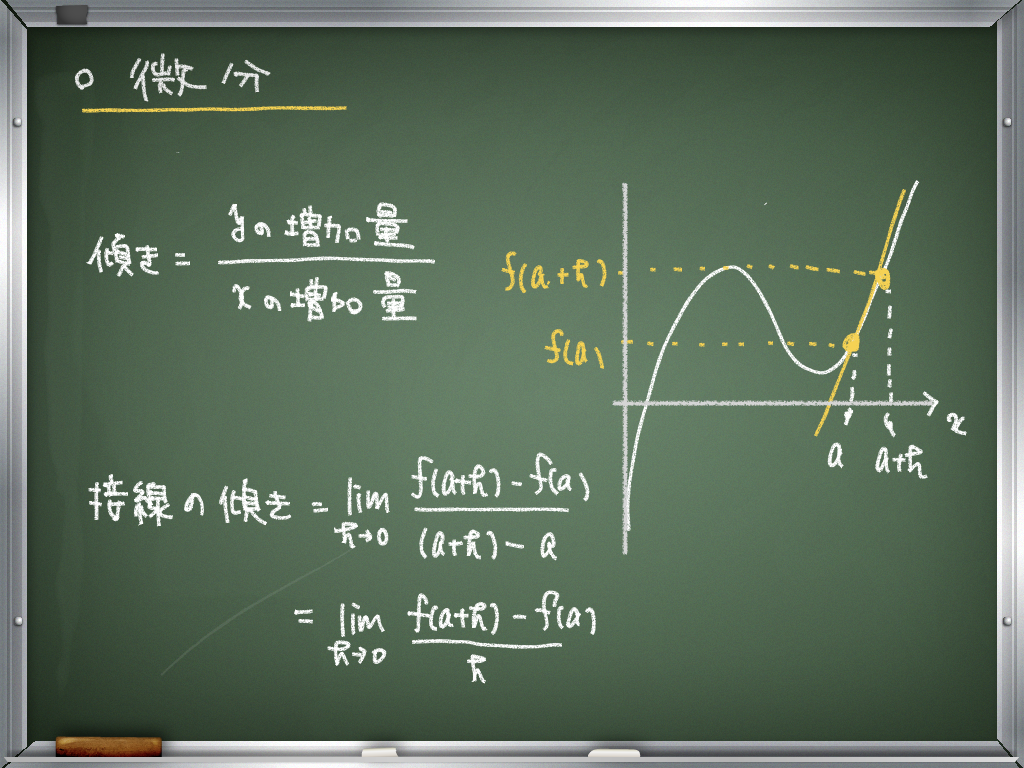
また導関数は以下のように定義できる．

導関数とは，接点の\(x \) 座標を代入すれば，その点での接線の傾きが出るものだ．

この導関数を増減表などの時に用いていたのだ．

\( \sin \) の微分

では導関数の定義にしたがって\( y=\sin x \) という関数を微分してみる．
$$y’=\lim_{h\rightarrow 0}\frac{\sin(x+h)-\sin x}{h}$$

$$=\lim_{h\rightarrow 0}\frac{\sin x\cos h +\cos x\sin h -\sin x}{h}$$

$$=\lim_{h\rightarrow 0}\frac{\sin x (\cos h -1 )+\cos x \sin h}{h}$$

$$=\lim_{h\rightarrow 0}\sin x\frac{\cos h-1}{h}+\cos x\frac{\sin h}{h}$$

2行目では加法定理を用いている．

3行目ではくくれるものはくくっている．

4行目では極限に関連する部分と関連しない部分をわかりやすくしている．

しかしながらここで問題が起きる．

$$ \lim_{h\rightarrow 0}\frac{\cos h-1}{h}\hspace{3mm},\hspace{3mm} \lim_{h\rightarrow 0}\frac{\sin h}{h} $$
この上の二つの極限は求めづらいのだ．

\( \frac{\cos h-1}{h} \) と\( \frac{\sin h}{h} \) はそれぞれについて\( h \) を0 に限りなく近づけると分母も分子も0に近づく．

極限において\( \frac{0}{0} \) の形は時と場合によって値が異なる．

そのためそれぞれを求める必要がある．

今回は都合上$$ \lim_{h\rightarrow 0}\frac{\sin h}{h} $$ から先に求める．

\(\displaystyle{\lim_{h\rightarrow 0}\frac{\sin h}{h}}\)

今回ははさみうちの原理を用いる．

ざっくりいうと\( 3\leq x \leq 3\) とわかれば，\( x=3 \) となる原理だ．

どのように挟むかというと以下の図を用いる．

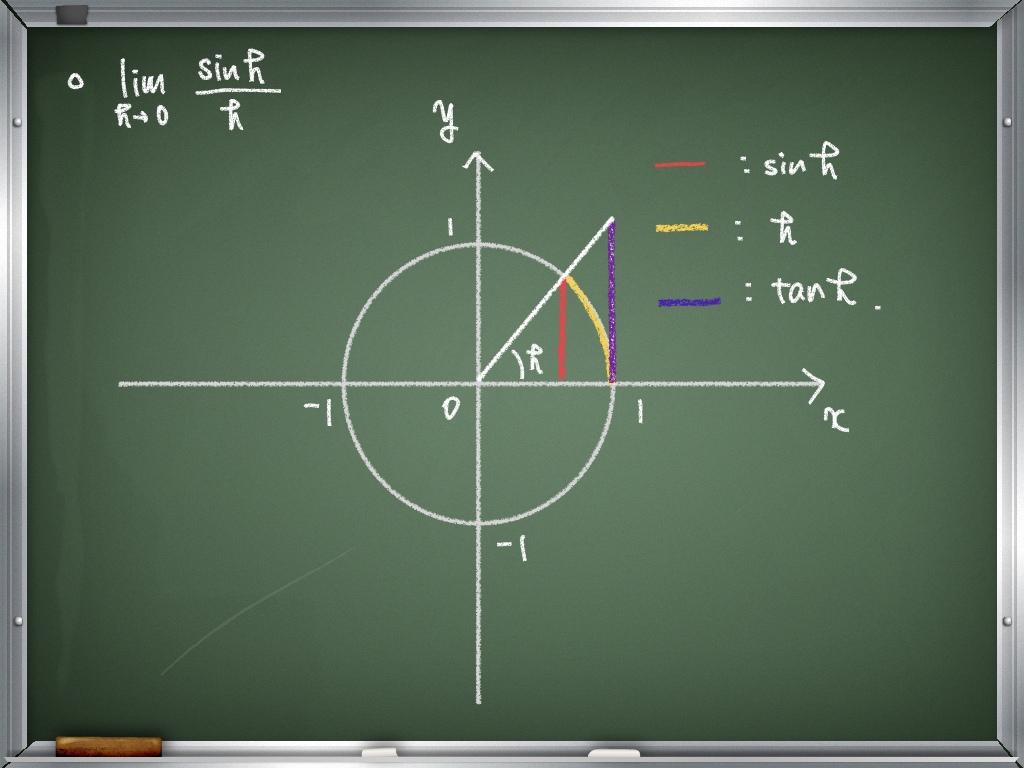
この図から分かるように長さを比較すると\( \sin h<h<\tan h \) となる。

これを式変形する．

$$\sin h <h<\tan h $$

相互関係を使う。
$$\sin h<h <\frac{\sin h}{\cos h}$$

\(\sin h\) で割る。

$$1<\frac{h}{\sin h} <\frac{1}{\cos h}$$

分母分子逆転すると、それぞれ正なので不等号も逆転する。

$$1>\frac{\sin h}{h} >\cos h$$

$$\cos h <\frac{\sin h}{h} <1$$

ここで極限をとる。

$$\lim_{h\rightarrow 0} \cos h \leq \lim_{h\rightarrow 0} \frac{\sin h}{h} \leq 1$$

$$ 1\leq \lim_{h\rightarrow 0} \frac{\sin h}{h} \leq 1$$

はさみうちの原理によって導ける。

$$\lim_{h\rightarrow 0} \frac{\sin h}{h}=1$$

これにより求めることができた。

\(\displaystyle{\lim_{h\rightarrow 0}\frac{\cos h-1}{h}}\)

今回なぜ\(\lim_{h\rightarrow 0} \frac{\sin h}{h}=1\)を先に求めたかというとこれを用いるからだ。

早速式変形に移る。

$$\displaystyle{\lim_{h\rightarrow 0}\frac{\cos h-1}{h}}$$

ここで\( \frac{\sin h}{h} \) を作ると，うまいこと1になってくれることを知っている．

そこで\( \cos h \) を\( \sin h \) にうまく変えたいという願望が生まれる．

そこで相互関係を用いるために，以下のように分母分子に\( \cos h+1\) をかけて変形していく．

$$\displaystyle{\lim_{h\rightarrow 0}\frac{\cos h-1}{h}=\lim_{h\rightarrow 0}\frac{(\cos h-1)(\cos h+1)}{h(\cos h+1)}}$$

$$\displaystyle{\hspace{12mm}=\lim_{h\rightarrow 0}\frac{\cos^2 h-1}{h(\cos h+1)}}$$

$$\displaystyle{\hspace{16mm}=\lim_{h\rightarrow 0}\frac{-(1-\cos^2 h)}{h(\cos h+1)}}$$

$$\displaystyle{\hspace{12mm}=\lim_{h\rightarrow 0}\frac{-(\sin^2 h)}{h(\cos h+1)}}$$

$$\displaystyle{\hspace{30mm}=\lim_{h\rightarrow 0}\frac{-(\sinh)}{h} \frac{\sin h}{(\cos h+1)}}$$

$$\displaystyle{\hspace{-3mm}=-1\cdot 0=0}$$

となる．

これより求めることができた．

再び本題へ

\( y=\sin x \) を微分してみると以下のようになった．
$$y’=\lim_{h\rightarrow 0}\sin x\frac{\cos h-1}{h}+\cos x\frac{\sin h}{h}$$

そして以下の二つの重要な極限を求めた．

これより\( y=\sin x \)を微分は以下の結果になる．

$$y’=\lim_{h\rightarrow 0}\sin x\cdot 0+\cos x \cdot 1=\cos x$$

よって\(\sin x\) の微分は\( \cos x\) となる．

まとめ