はじめに
多様体とは、位相空間に座標近傍系を加えて「微分」を定義したものだった。
(詳しくは多様体とは何か?)
では微分とは何だろうか?
関数\(f:\mathbb{R}\rightarrow \mathbb{R}\)について\(x=c\)で微分するとは、
\(\displaystyle{f'(c)= \lim_{h \to 0} \frac{f(c+h)-f(c)}{h} }\)を出すことである。
このように一変数から実数への微分は高校の時から慣れ親しんできた。
では私たちの対象にしたい空間,すなわち2次元は3次元,…上はどのように定義するのか。
まずは一変数
\(\displaystyle{f'(c)= \lim_{h \to 0} \frac{f(c+h)-f(c)}{h} }\)
今回学ぶ \(C^k\) 級という概念は誤解を恐れずざっくりいうと
「何回きれいな微分できるか。」という話だ。
もっと具体的に説明する。
まず写像 \(f\) が \(C^0\) 級であるとは, \(f\) が連続であることだ。
そして一変数において \(f\) が \(C^1\) 級であるとは,
\(f\) が 微分可能で、\(\frac{\partial f}{\partial x}\) が\(C^0\) 級,すなわち連続であることだ。
あとは帰納的に\(f\)が\(C^k\) 級であるとは,
\(f\) が 微分可能で、\(\frac{\partial f}{\partial x}\) が\(C^{k-1}\) 級であることだ。
以下にまとめておく。
\(f\) が\(C^0\) 級であるとは, \(f\) が連続であること.
\(f\)が\(C^k\) 級であるとは,\(f\) が微分可能で、\(\frac{\partial f}{\partial x}\) が\(C^{k-1}\) 級であること.
(特に\(f\)が\(C^1\) 級であるとは,\(f\) が微分可能で、\(\frac{\partial f}{\partial x}\) が\(C^{0}\) 級,すなわち連続であること.)
多変数関数について
一変数関数\( f:\mathbb{R} \rightarrow \mathbb{R} \) について考察する。
これはxという実数に対してyという実数を対応させるということだ。
そして実数はしばしば数直線として視覚的にわかりやすく表現される。
ここで微分において重要な「少しずらす」という操作について考えてみる。
あなたが直線上にいる時(綱渡りをしているとき)に「少しずれて!」と言われたとしたら
果たしてどうするだろうか。
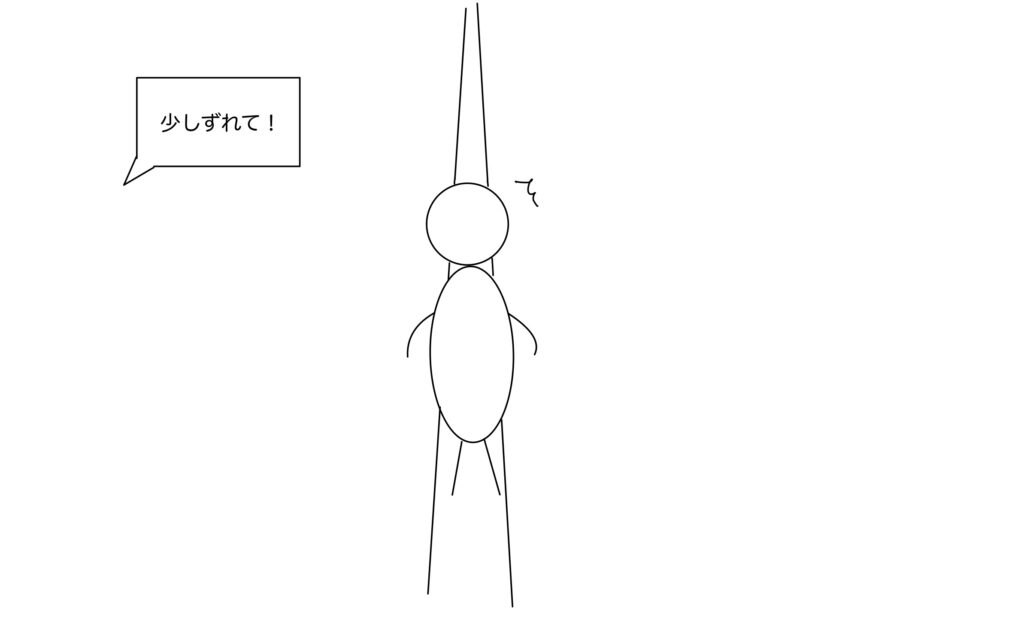
もちろんはみ出すことはできないので、前か後ろかの2択しかない。
そのため、私たちは正にずらすときと負にずらすときの2択だけを考えればよかった。
しかしながら多変数を考えるとこうも上手くはいかない。
例えば二変数関数 \( f:\mathbb{R}^2\rightarrow \mathbb{R} \)について考えてみる。
先程は一次元を数直線と捉えたが、今度は平面になる。
すると「少しずれて!」と言われると縦方向に加え、横方向もズレることができる。
それだけではない。右斜め前もOKで南南東もOKになる。
さらには、なみなみに沿って少しずれることも可能となる。
つまり、二変数になると2択だけでなく、あらゆる近づけ方を確認しなければならない。
1変数から多変数に変わるだけで、選択肢は一気に無数になる。
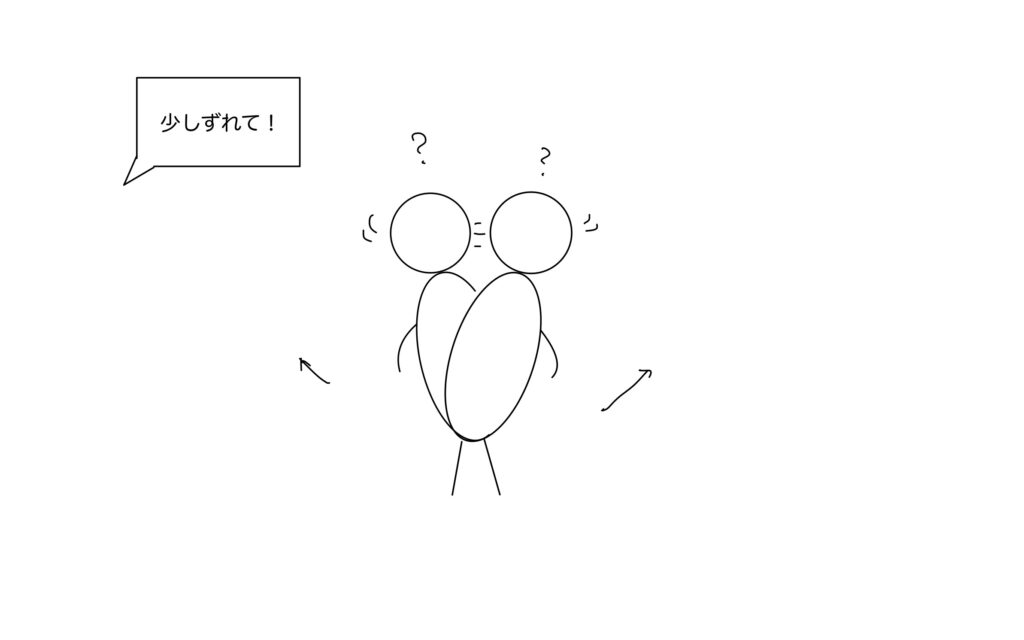
この平面上の全方向に微分可能ですよ。という主張が全微分という定義である。
\(f(x,y)\) が\((a,b)\) で全微分可能であるとは,
次の条件を満たす定数\(A,B\) と\(\epsilon (x.y)\) が存在することである.
・\(f(x,y)=f(a,b)+A(x-a)+B(y-b)\)
\(\hspace{30mm}+\sqrt{(x-a)^2+(y-b)^2} \epsilon (x,y)\)
・\(\epsilon (x,y)\) は連続で\((x,y) \rightarrow (a,b)\)のとき,\(\epsilon (x,y) \rightarrow 0\)
ではどのように対処すれば良いのか?
これだけみると多変数関数の近づけ方は無数にあるので、永遠にわからない気がする。
しかしながら、下に書く定理のおかげで私たちは多変数に希望を見出せる。
各方向に偏微分可能なら、全微分可能である。
この主張は「2方向だけで微分可能性を確かめれば、平面のどんなずらし方でも微分できる」
というものすごい主張である。
無数にある選択肢をx軸方向とy軸方向のたった2方向のみで確かめてしまえばいいのだ。
すなわち\(f\) が\(\frac{\partial f}{\partial x}\) と\(\frac{\partial f}{\partial y}\) がwell-definedならば、\(f\) が全微分可能なのだ。
多変数のC^k級
全微分可能かどうかは各方向が微分可能であるかどうかが重要だった。
これより一変数の時に習って多変数の時を定義する。
\( f:\mathbb{R}^m \rightarrow \mathbb{R} \) が \(C^0\) 級であるとは, \(f\) が連続であること.
\(f\)が\(C^k\) 級であるとは,\(f\) が各方向微分可能で、\(\frac{\partial f}{\partial x_i}(i=1,\cdots ,m)\) が\(C^{k-1}\) 級であること.
(特に\(f\)が\(C^1\) 級であるとは,\(f\) が各方向微分可能で、\(\frac{\partial f}{\partial x_i}\) が\(C^{0}\) 級,すなわち連続であること.)
このように定義することにより、多変数の\( C^k \) 級を定義することができた。
終わりに
今回はとても厳密性に欠けるような説明である。
例えば、1変数の微分はそもそもどのように定義できるのか、
全微分の可能性の定理をどのように証明するのかなど説明されていない部分がある。
ただここを学んでいるときに私は訳がわからなかったという経験があるので、
まず直観や見方をサラーっと勉強するためのものとして書いた。
ご覧になられた方のサポートになれれば嬉しい。
\(\)
コメント