P.N.nikingさんから以下のようなお便りをいただきました。
ご質問ありがとうございます。
質問は以下から受け付けておりますので、よろしければご連絡ください。
(ご質問がある方)
位相空間\((X,\mathcal{O})\)とその部分空間\((A,\mathcal{O}_A)\)について
\((X,\mathcal{O})\)がコンパクトで部分集合\(A\)が\(X\)において閉集合ならば、
\((A,\mathcal{O}_A)\)もコンパクトというのは本当でしょうか。
気になって朝も起きられません。
くれぐれも体にはご自愛ください。
おさらい
相対位相、コンパクトの定義をおさらいしておく。
(詳しくは相対位相、位相におけるコンパクト性)
\((X,\mathcal{O})\)を位相空間とし、部分空間\(A \subset X\)を考える。
この時、Aに\(\mathcal{O}_A=\{O \cap A| O \in \mathcal{O} \}\)という位相をいれる。
この時、\(\mathcal{O}_A\)を相対位相といい、\((A,\mathcal{O}_A)\)を\((X,\mathcal{O})\)の部分空間とよぶ。
ここでのポイントは「\(X\)の開集合と\(A\)の交わりを\(A\)の開集合とするよ。」ということである。
位相空間\((X,\mathcal{O}_X)\)がコンパクトであるとは、
\(X\)の任意の開被覆\(\{O_\lambda |\lambda \in \Lambda \}\)について
その有限部分開被覆\(\{O_i | i \in A \} \subset \{O_\lambda |\lambda \in \Lambda \}\)が存在することである。
ここでのポイントは「好きに開被覆を持ってきてもエコな人が捌くと有限個になること」である。
今回の問いの難しさ
今回の問いがなぜ難しいのかというと、開集合と開被覆の所在がごちゃごちゃになることだ。
言い換えると、\(A\)の開集合(開被覆)なのか\(X\)の開集合(開被覆)なのかが曖昧になる。
そしてさらにややこしいのが、開被覆は要素が開集合であることである。
この2点に注意をしながら問題をみていく。
問題と証明の流れ
位相空間\((X,\mathcal{O})\)とその部分空間\((A,\mathcal{O}_A)\)について
\((X,\mathcal{O})\)がコンパクトで部分集合\(A\)が\(X\)において閉集合ならば、
\((A,\mathcal{O}_A)\)もコンパクトであることを示せ。
今回示すことは、\((A,\mathcal{O}_A)\)がコンパクトであることだ。
これより示すべきことは「\(A\)の任意の開被覆について有限部分開被覆が存在すること」だ。
つまり証明のスタートは
「\(A\)の任意の開被覆\(\mathcal{A}=\{O_\lambda \cap A |\lambda \in \Lambda \}(^{\forall} \lambda \in \Lambda についてO_\lambda \in \mathcal{O})\)について考える」
と宣言することだ。
これは\(A\)の開被覆であるから\(A\)における開集合が要素となる。
そして相対位相の定義であることを踏まえると、今回の開被覆はあのような形であるべきだ。
そして証明のゴールは「\(A\)の開被覆\(\mathcal{A}=\mathcal{A}=\{O_\lambda \cap A |\lambda \in \Lambda \}\)が有限部分開被覆を持つ。」と言い切ることだ。
\(A\)の任意の開被覆\(\mathcal{A}=\{O_\lambda \cap A |\lambda \in \Lambda \}\)について考える。
と宣言した後にこのままではどのようにゴールにたどり着くのかわからない。
そこで、仮定の登場である。
仮定の確認
今回大きく目につく仮定は\((X,\mathcal{O})\)がコンパクトであることだ。
言い換えると、「\(X\)の開被覆を持ってきてくれたら有限個に捌きますよ。」
ということを仮定している。
これは、最終的なゴールである有限部分開被覆の手助けになってくれそうな匂いがする。
しかし、私たちが考えている開被覆は\(A\)の開被覆であり、\(X\)の開被覆でない。
つまり図で書くとこのような状況となっている。
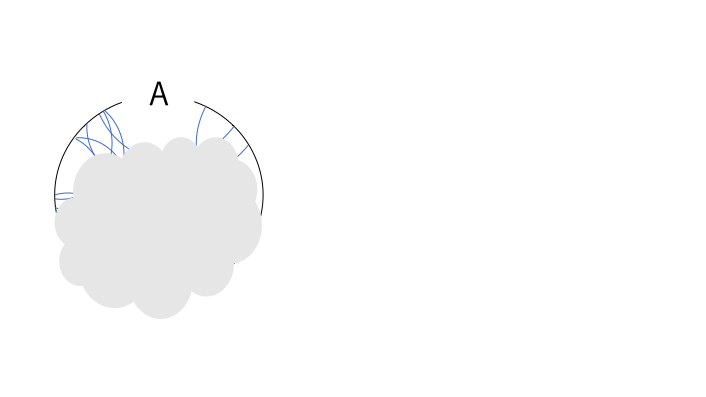
\(A\)は濃度がわからない\(A\)の開被覆で覆われている。
(雲で隠しているのは、開集合が有限個か無限個かわからない意味を込めている。)
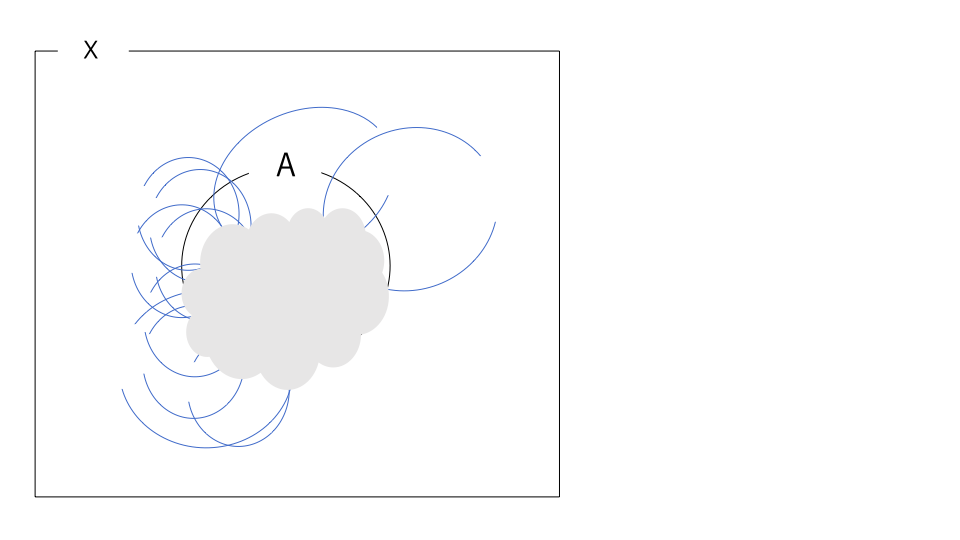
しかし、この図のように必ずしもX全体を被覆しているとは限らないのだ。
これでは、\((X,\mathcal{O})\)がコンパクトであるという仮定を発動できない。
そこで他に仮定はないかと探してみると、\(A\)が\(X\)で閉集合という仮定がある。
これは\(X-A\)が\(X\)で開だと言ってくれている。

図でいうと、この黄色い部分は\(X\)で開集合だと言っている。
今の悩みのたねが「\(X\)全体を被覆しているとは限らず、\((X,\mathcal{O})\)がコンパクトであるという仮定を発動できない。」だったことを思い出すと、
\(A\)の全ての開被覆の要素と\(X-A\)を使えば、\(X\)を覆う事ができるというアイデアが浮かぶ。
しかし\(A\)の開被覆の要素は\(A\)での開集合であって、\(X\)での開集合ではない。
だがその疑問は相対位相であったことを思い出せば、\(\{O_\lambda \cap A |\lambda \in \Lambda \}\)の\(O_\lambda\)部分のみを取り出せば解消される。
これで、ようやく一点の曇りもなく\(X\)の開被覆\(\{O_\lambda |\lambda \in \Lambda\}\cup\{X-A\}\)を考える事ができる。
そして\((X,\mathcal{O})\)がコンパクトであるという仮定がようやく発動できて、
\(\{O_\lambda |\lambda \in \Lambda\}\cup\{X-A\}\)は有限部分開被覆
\(\{O_i | i=1,2,3,\cdots n\} (\cup\{X-A\})\)
後ろの\((\cup\{X-A\})\)については、有限個に捌くときに外されるかどうかが曖昧である。
しかし、私たちのゴールは「\(A\)の開被覆\(\mathcal{A}=\{O_\lambda \cap A |\lambda \in \Lambda \}\)が有限部分開被覆を持つ。」である。
そのことを思い出すと、
「\(\{O_i \cap A|i=1,2,3,\cdots ,n\}\)という有限部分開被覆を持つ」が何よりの最重要事項であって、
後ろに\((\cup\{X-A\})\)がつこうがつかまいがどっちでもいいのだ。
解答例
\(A\)の任意の開被覆\(\mathcal{A}=\{O_\lambda \cap A|\lambda \in \Lambda\}\)について考える。(\(^{\forall}\lambda \in \Lambda \)について\(O_\lambda \in \mathcal{O}\)。)
\(A\)は\(X\)で閉集合であるから、\(X-A\)は\(X\)で開集合となる。
このことから\(\{O_\lambda| \lambda \in \Lambda \}\cup \{X-A\}\)は\(X\)の開被覆となる。
\((X,\mathcal{O})\)はコンパクトであるから、\(\{O_\lambda| \lambda \in \Lambda \}\cup \{X-A\}\)は\(X\)は有限部分開被覆\(\{O_i| i=1,2,3,\cdots ,n \}(\cup \{X-A\})\)を持つ。
このことから\(A\)の開被覆\(\mathcal{A}=\{O_\lambda \cap A|\lambda \in \Lambda\}\)は有限部分開被覆\(\{O_i\cap A| i=1,2,3,\cdots ,n \}\)を持つ。
したがって\((A,\mathcal{O}_A)\)もコンパクトである。
おまけ
開集合や開被覆は位相空間の話で当たり前のように持ち出されるが、
どこの開集合か開被覆かというところは見落としがちである。
何か問題が解けない時には、どこの開集合か開被覆かをチェックすると問題が解けることがある。
\(\)
コメント