積位相が基底で定義される理由

積空間の定義は以下のようであった。(詳しくは積空間)

このように積位相は基底によって定義される。

ではなぜ基底によって定義されたのかを見ていく。

積位相について

\((X,\mathcal{O}_X),(Y,\mathcal{O}_Y)\)が位相空間で直積集合\(X \times Y\)に位相を定めるのが、目標。
(その理由については積空間を参照。)

位相を定めるということは、「開集合が、これとこれとこれと…」と要求することだ。

そして直積集合\(X \times Y\)の開集合を定めるアイデアとして、
「\(X\)から開集合\(U\)をとって、\(Y\)から開集合\(V\)をとってきて、\(U\times V\)を開集合とする。」
というものは思い浮かびそうなものだ。

この考え方「\(\{U\times V| U \in \mathcal{O}_X,V \in \mathcal{O}_Y \}\)」を位相ではなく、なぜ基底にしたのかというのは位相の定義を確認するとわかる。

位相の確認

位相の定義は以下のようであった。(詳しくは位相)

では「\(\{U\times V| U \in \mathcal{O}_X,V \in \mathcal{O}_Y \}\)」について位相の条件をそれぞれ確認する。

空集合と全体集合を含んでいるかというチェック。

\((X,\mathcal{O}_X),(Y,\mathcal{O}_Y)\)は位相空間だから\(\emptyset \in\mathcal{O}_X,\emptyset \in \mathcal{O}_Y)\)が成り立つ。

これより\(\emptyset=\emptyset \times \emptyset \in \{U\times V| U \in \mathcal{O}_X,V \in \mathcal{O}_Y \}\)となる。

\((X,\mathcal{O}_X),(Y,\mathcal{O}_Y)\)は位相空間だから\(X \in\mathcal{O}_X,Y \in \mathcal{O}_Y\)が成り立つ。

これより\(X \times Y \in \{U\times V| U \in \mathcal{O}_X,V \in \mathcal{O}_Y \}\)となる。

よって(1)はOK。

(2)は2つの開集合の交わりも開集合となるかというチェック。

しかし、ベン図では積集合の概念は掴みづらい。
ここで、「\(\mathbb{R}^2\)のときどうしてたっけ？」と考えると下の図の意味がわかる。

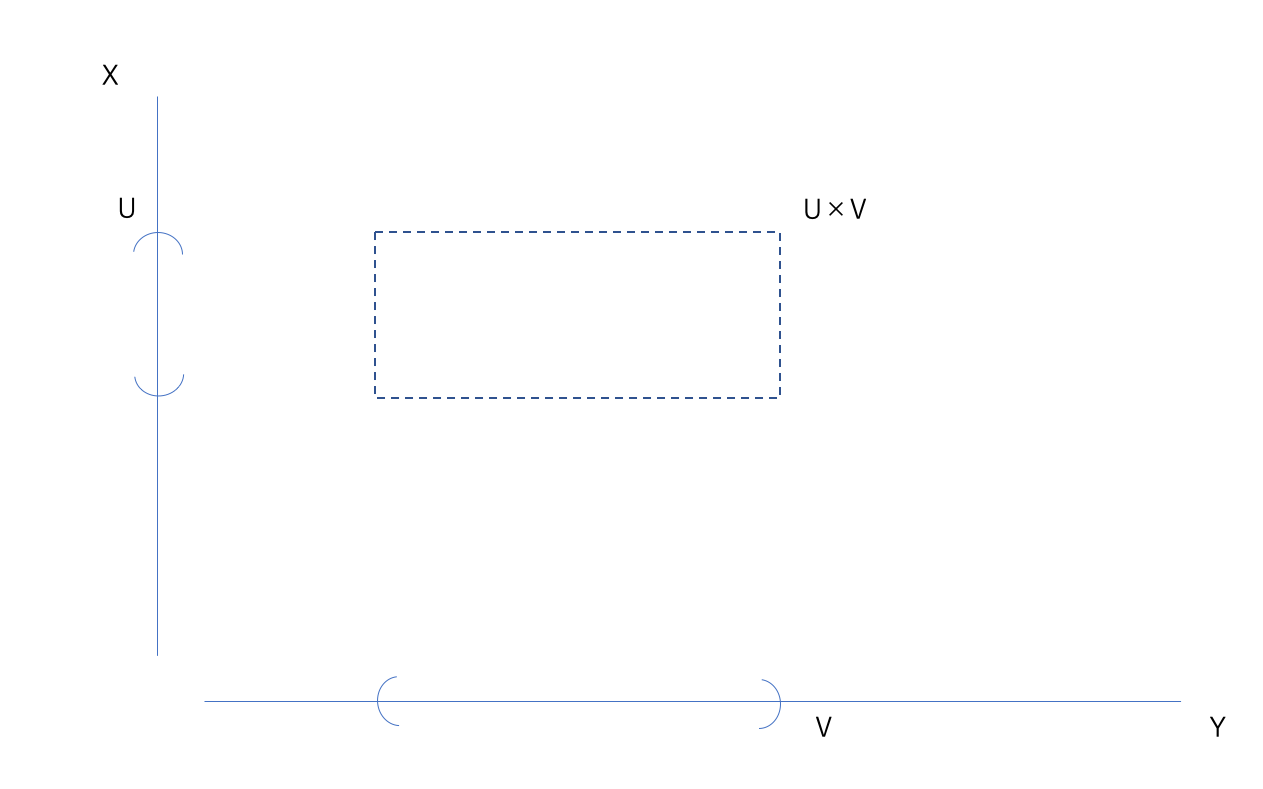
ベン図では集合を円や四角形で表していたが、上のように集合を直線で考える。
そうした時に、直積集合を理解しやすくなった。

さて、ここで\(U_1 \times V_1,U_2 \times V_2 \in \{U\times V| U \in \mathcal{O}_X,V \in \mathcal{O}_Y \}\)の交わりを考える。

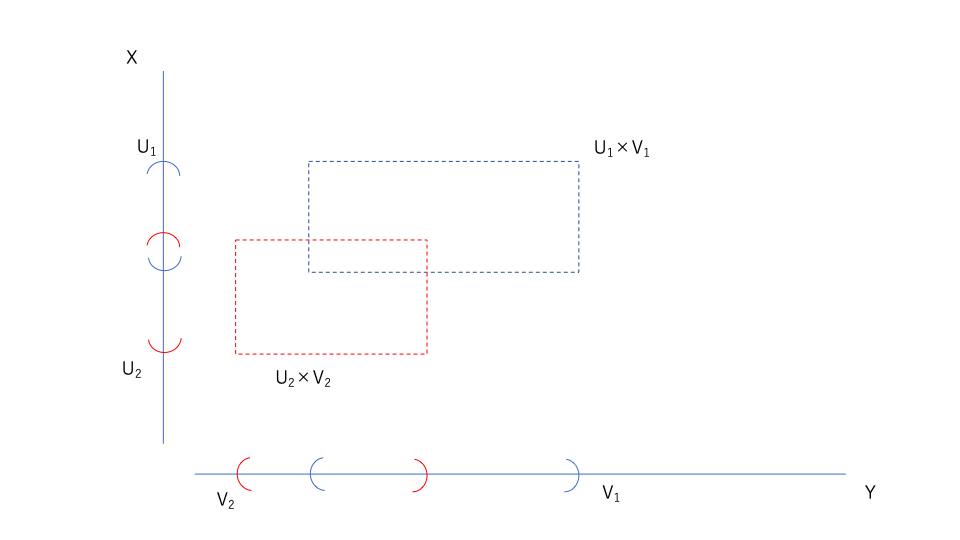
これは、\(U_1 \times V_1,U_2 \times V_2\)の図だが、その交わりとは下の図の黄色い部分である。

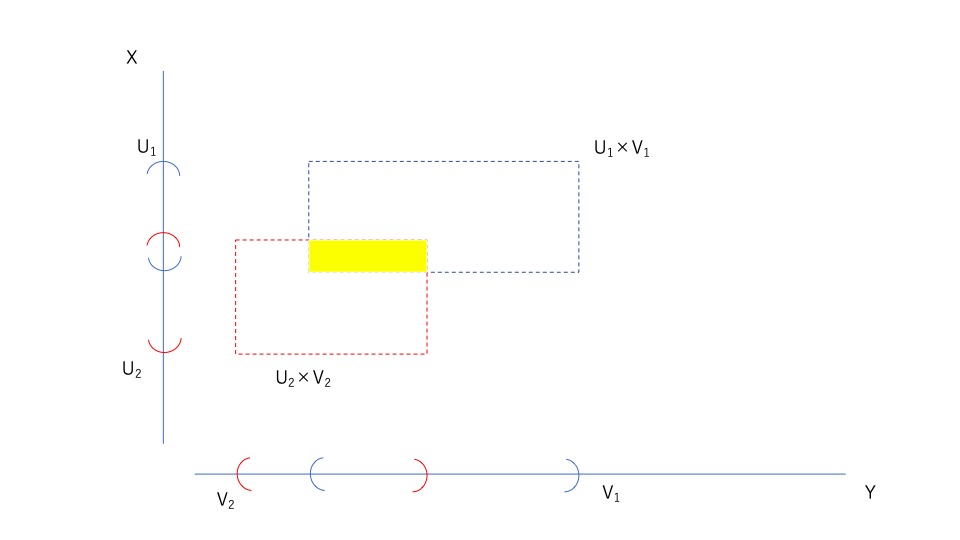
この図からイメージできるように、\(U_1 \times V_1,U_2 \times V_2\)の交わりは
\(U_1 \cap U_2 \times V_1 \cap V_2\)と見ることができる。

\(U_1 \cap U_2\)は、\((X,\mathcal{O}_X)\)が位相空間であることを踏まえて、
開集合と開集合の交わりは開集合であるから、\(U_1 \cap U_2\)も開集合である。

同様に\(V_1 \cap V_2\)も開集合である。

このことから\(U_1 \cap U_2 \times V_1 \cap V_2\)は\(X\)の開集合と\(Y\)の開集合の交わりとなる。

よって\(U_1 \cap U_2 \times V_1 \cap V_2 \in \{U\times V| U \in \mathcal{O}_X,V \in \mathcal{O}_Y \}\)

これより(2)もOK.

(3)では開集合を好きなだけとってきて和集合をとってきても開集合になることをチェック。

さて、ここで先ほどの\(U_1 \times V_1,U_2 \times V_2\)について考える。

\(U_1 \times V_1 \cup U_2 \times V_2\)を考えると、以下の黄色の部分になる。

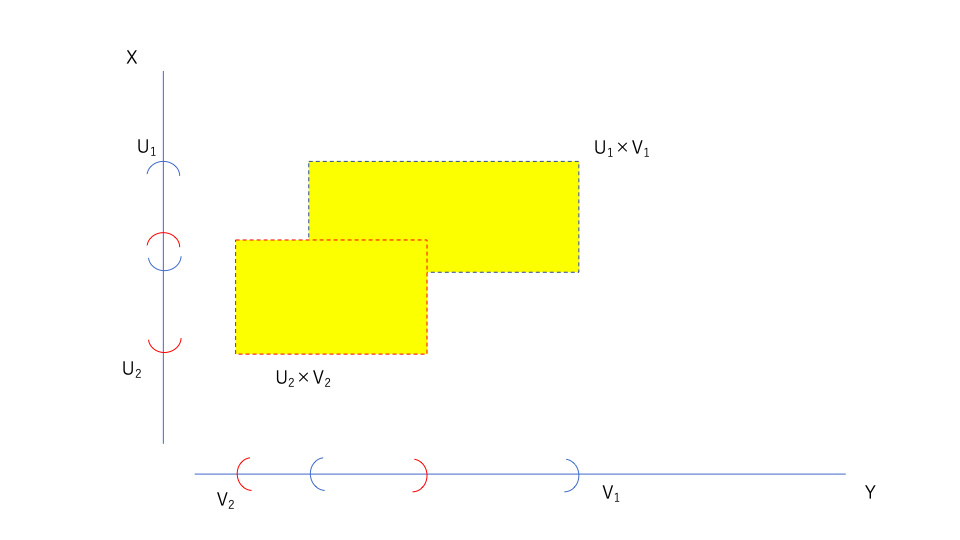
先ほどは、\(U_1 \times V_1 \cap U_2 \times V_2 =U_1 \cap U_2 \times V_1 \cap V_2\)とすることができた。

今回も\(U_1 \times V_1 \cup U_2 \times V_2 =U_1 \cup U_2 \times V_1 \cup V_2\)とできたら万歳。

しかし\(U_1 \cup U_2 \times V_1 \cup V_2\)は以下のようになる。

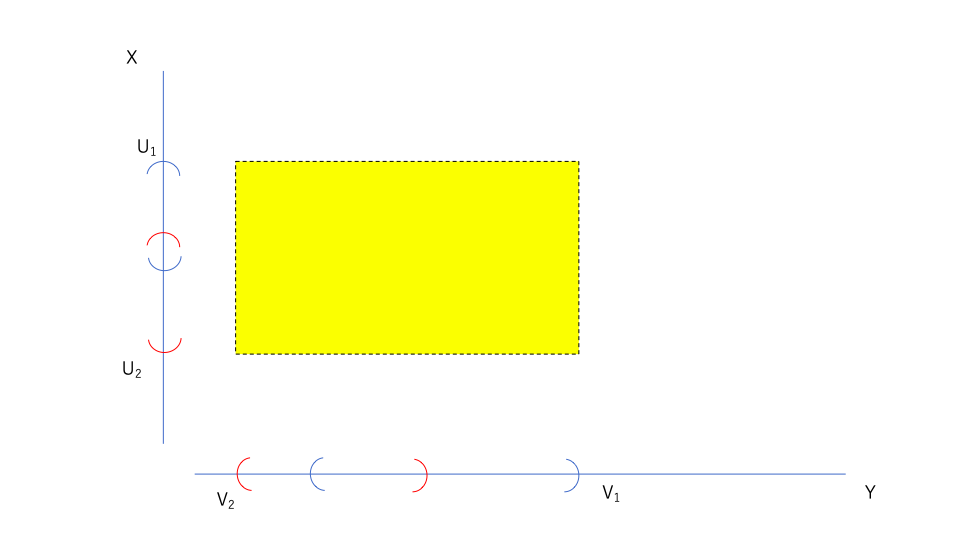
\(U_1 \times V_1 \cup U_2 \times V_2 =U_1 \cup U_2 \times V_1 \cup V_2\)とはならない。

このように、\(U_1 \times V_1 \cup U_2 \times V_2\)を開集合\(\times\)開集合の形で表すことはできない。

だから、(3)は満たすことができない。

最後のまとめ

「\(\{U\times V| U \in \mathcal{O}_X,V \in \mathcal{O}_Y \}\)」は位相の条件(1)(2)は満たすが、(3)は満たさない。

このままでは、せっかくすんなりと浮かぶようなアイデア
「Xの開集合とYの開集合の直積集合を開集合とする。」を手放してしまうことになる。

このような状況を打破するために生まれた概念を覚えているだろうか。

そう、基底である。(詳しくは基底をチェック)

だから、積位相では

と定めている。