\((X,\mathcal{O})\)を位相空間とし、部分空間\(A \subset X\)を考える。
この時、Aに\(\mathcal{O}_A=\{O \cap A| O \in \mathcal{O} \}\)という位相をいれる。
この時、\(\mathcal{O}_A\)を相対位相といい、\((A,\mathcal{O}_A)\)を\((X,\mathcal{O})\)の部分空間とよぶ。
今回の相対位相は、1つの位相空間の部分集合を考えるというものだ。
定義解説
「Aの位相は、元々の開集合とAとの交わりをそれぞれ考え、それを開集合としましょうね。」
と定義する。
これがちゃんと位相になっているかは、位相の3つの条件をクリアしているかを確認すれば良い。
(詳しくは位相の記事で。)
(1)\( \emptyset ,X \in \mathcal{O}\)
元の親の世界\((X,\mathcal{O})\)には、位相に\(\emptyset ,X\)が入っている。
これとAとの交わりを考えると、\(\emptyset \cap A=\emptyset ,X \cap A=A\)となる。
これより子の世界\((A,\mathcal{O}_A)\)にも、空集合と全体集合が入っているので、(1)はクリア。
(2)\(^{\forall}O_1,O_2 \in \mathcal{O}\)について\(O_1 \cap O_2 \in \mathcal{O}\)
\(\mathcal{O}_A=\{O \cap A| O \in \mathcal{O} \}\)から任意に2個開集合をとる。
その2つは、\(O_1\cap A,O_2\cap A\)(\(O_1,O_2 \in \mathcal{O}\))と書ける。
この2つの交わりもちゃんと\(\mathcal{O}_A\)の中に入っておけば(2)はクリア。
\((O_1\cap A) \cap (O_2\cap A)=(O_1 \cap O_2) \cap A\)となる。
\(O_1 \cap O_2\)は親の世界が位相空間であり、(2)の条件は当然クリアするので、
親の世界で開集合となる。
親の世界\((X,\mathcal{O})\)で開集合であるものとAとの交わりは\(\mathcal{O}_A\)に入っている。
よって\((O_1\cap A) \cap (O_2\cap A)=(O_1 \cap O_2) \cap A \in \mathcal{O}_A\)となる。
これより、(2)もクリア。
(3)\(^{\forall}\{O_\lambda \}_{\lambda \in \Lambda} \subset \mathcal{O}\)について\( \cup_{\lambda \in \Lambda} O_\lambda \in \mathcal{O}\)
\(\mathcal{O}_A=\{O \cap A| O \in \mathcal{O} \}\)から任意に開集合を好きな分だけとる。
その和集合\(\cup_{\lambda \in \Lambda} (O_\lambda \cap A)\)が\(\mathcal{O}_A\)に入っておけば(3)はクリア。
\(\cup_{\lambda \in \Lambda} (O_\lambda \cap A)= \cup_{\lambda \in \Lambda}O _\lambda \cap A\)となり、(3)もクリア。
これは記号ではわかりづらいので、図を用いて説明する。
まず\(\cup_{\lambda \in \Lambda} (O_\lambda \cap A)\)の図はこちら。
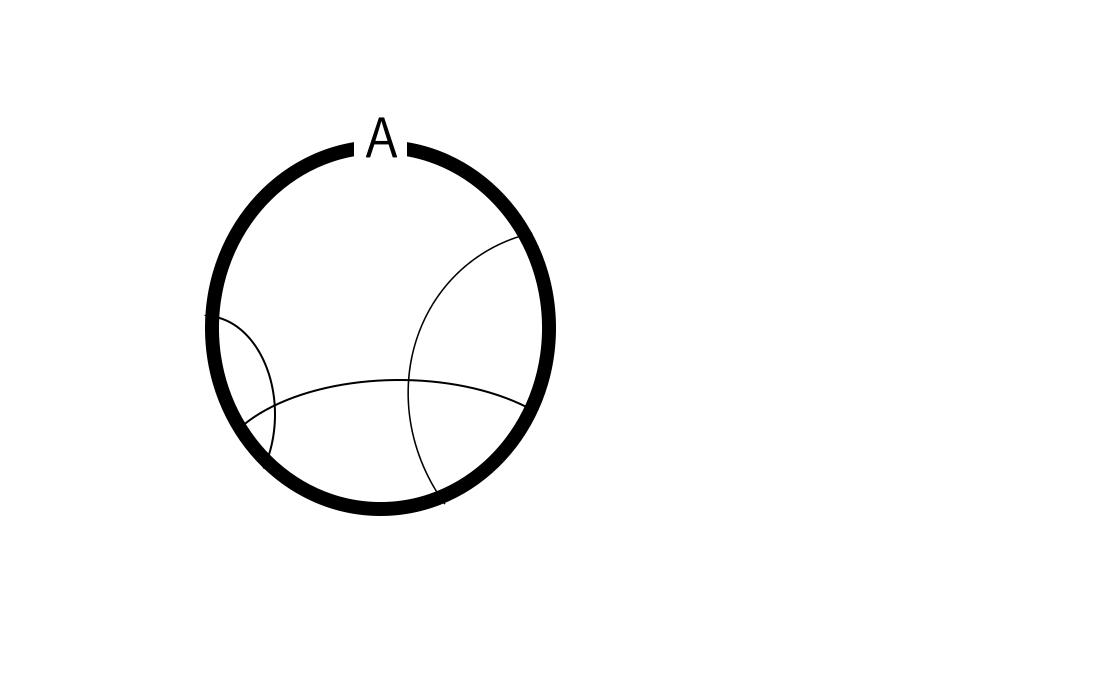
このように\(A\)の世界で、\(\cup_{\lambda \in \Lambda} (O_\lambda \cap A)\)を考えている。
これを\(\mathcal{O}_A\)の定め方から下の図のようにみることができる。
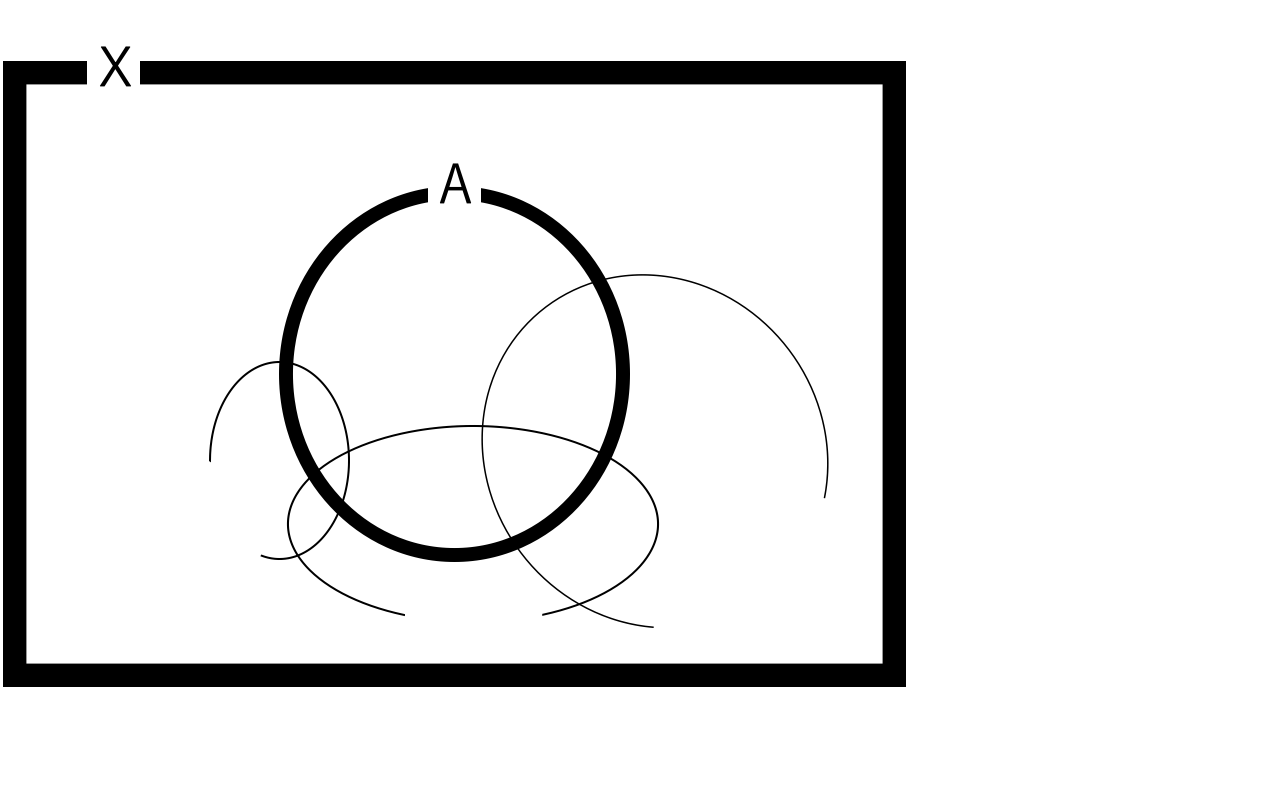
このように見て親の世界のみで下のように考える。
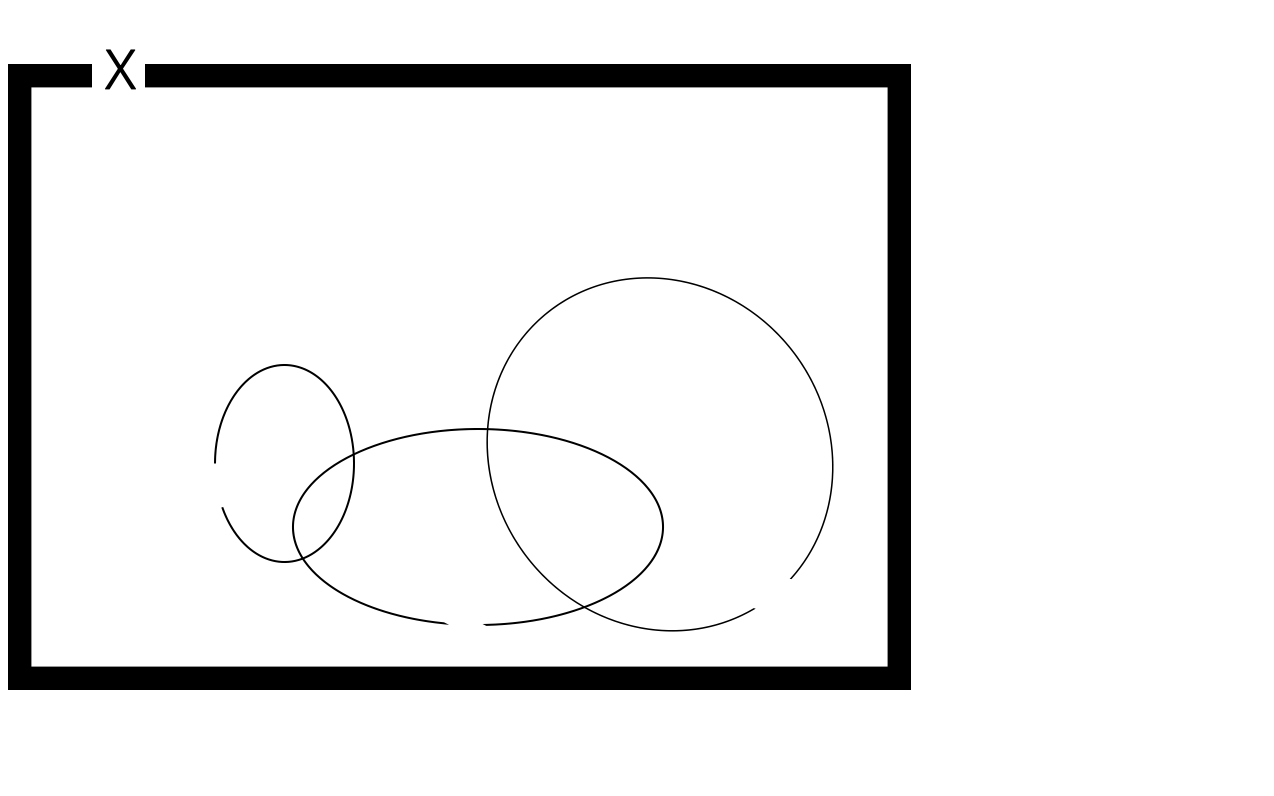
そうすると、\((X,\mathcal{O})\)は位相空間だから、この3つの和集合も開集合。
このことを踏まえ、以下の図を見ると「開集合とAとの交わりになっているよね。」とわかる。

よってこのことから(3)はクリア。
このことから相対位相は本当に位相であることがわかった。



コメント