はじめに
集合論と題して、集合の要素の個数という概念を一般化した濃度について学んできた。
今まで驚くべき事実と無限の恐ろしさについて触れてきた。
例えば、自然数と整数の個数が一緒だったり、自然数と有理数の個数が一緒という
直観に反する事実を目の当たりにしてきた。(詳しくは自然数と整数の濃度)
そして何もかも自然数の濃度と等しくなるのではないかと思ったその時、
初めて自然数の濃度よりも大きくなる実数の濃度が現れた。(詳しくは自然数と実数の濃度)
そこで、今回は実数と濃度が等しいものにはどんなものがあるのだろうかということを見ていく。
濃度の復習
集合全体の集まりにおいて,対等という同値関係による同値類を濃度という.
集合\(A\)に対し,\(A\)の濃度を\(|A|\)とかく.
\(A,B\)を集合とする.ある全単射\(f:A\rightarrow B\)が存在するとき,
\(B\)は\(A\)と対等であるという.(記号:\(A \sim B\))
同値類や対等という言葉が出てきて、やめたくなるかもしれない。
しかしながら一番覚えていて欲しいところは
「集合同士に全単射が1つであれば、その濃度は一緒です」という決め事である。
私たちは集合の包含関係(例:自然数は整数に含まれている)で個数を見がちだが、
数学では個数の一般化である濃度は全単射の存在で定めている。
その感覚と異なる定義なのだということを前提に実数の濃度を比較していく。
開区間(0,1)と実数
実数の濃度は自然数より大きい、ましてや有理数よりも大きいものなのに
\((0,1)\)というとても狭い範囲と濃度が一緒というのは驚くべき事実だ。
\((0,1)\)という有界な世界でも中には無限の要素が詰まっていることを教えてくれる。
さて、濃度が等しいかどうかは全単射が存在するかどうかだった。
今回の主役は高校生の頃に習った三角関数、特に\(\tan x\)である。
\(f:(0,1) \rightarrow \mathbb{R}\)を\(f(x)=\tan (\pi x-\frac{\pi}{2})\)と定める。
そうすると、これは全単射となっていることがわかる。
以下が全単射となっていることがわかりやすいグラフである。
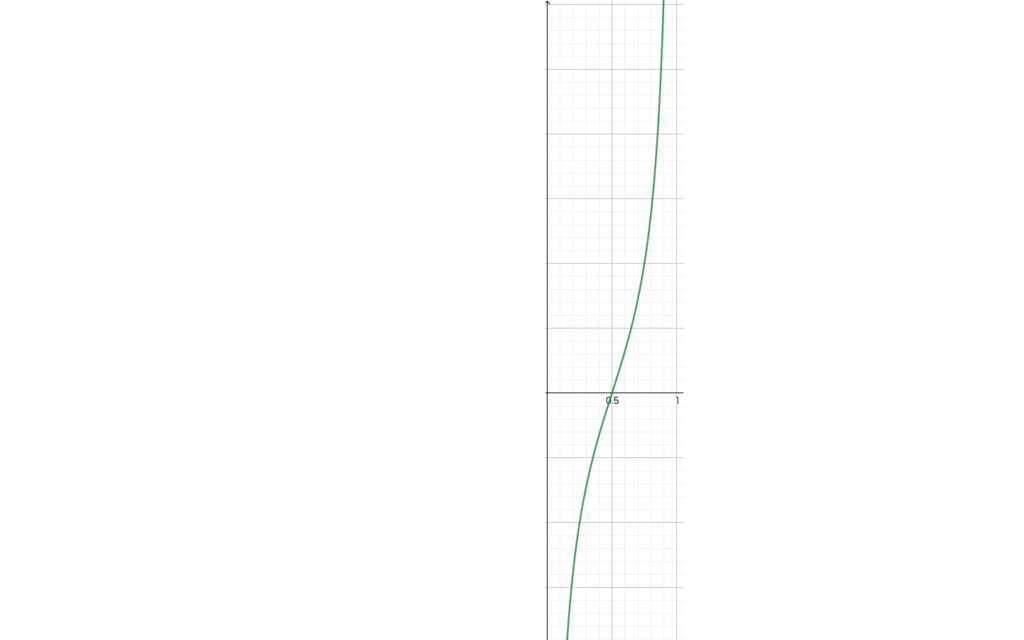
このことから\((0,1)\)と\(\mathbb{R}\)の濃度が等しいことがわかった。
閉区間[0,1]と実数

開区間(0,1)と実数の濃度が等しいなら、閉区間も等しいでしょ。
確かに、直観的にはそう言いたくなってしまう。
「その根拠は?」と言われると、集合の包含関係を考えているのではないだろうか。
すなわち\((0,1) \subset [0,1] \subset \mathbb{R}\)だから閉区間\([0,1]\)と\(\mathbb{R}\)の濃度が等しいと考えているだろう。
しかしながら集合の濃度は、集合の包含関係ではなく全単射を用いて定義している。
そのため、\(\mathbb{N}\subset \mathbb{Z}\)であるが、濃度は等しいという直観とは異なる事実があった。
だから今回の集合の包含関係のはさみうちにより濃度が等しいと結論づけるためには
証明が必要である。
実はその望みは叶えられていて、ベルンシュタインの定理と呼ばれている。
集合\(X,Y,Z\)について\(X \subset Y \subset Z\)が成り立っているとする
このとき\(X\)と\(Z\)の濃度が等しいならば,\(Y\)の濃度も等しい.
これによって\((0,1) \subset [0,1] \subset \mathbb{R}\)で\((0,1)\)と\(\mathbb{R}\)の濃度が等しいことから
\([0,1]\)の濃度と\(\mathbb{R}\)の濃度が等しいことがわかった。
終わりに
今回\([0,1]\)と\(\mathbb{R}\)の濃度が等しいことを言うためにベルンシュタインの定理を用いた。
次回はベルンシュタインの定理そのものの証明をしていく。
\(\)
コメント