はじめに
私は大学2年生のときに,初めて群というものを習った.
抽象的な定義に「これが何の役に立つの?」と思わず首をかしげた.
しかしながら,この基本群を習ったときに「こんなところに群があるのか!」と驚いた.
今回はこの基本群について説明していく.
位相空間の復習
私たちの感覚では道というのは,歩いてきたその足跡のようなものとして捉える.
しかしながら位相空間論における道の定義は写像であった.
\((X,\mathcal{O})\)を位相空間とする。
\(^{\forall}x_0,x_1 \in X\)について\(^{\exists}\alpha \colon I \rightarrow X\)(連続写像)\(\hspace{2mm}s.t.\hspace{2mm}\alpha (0)=x_0\hspace{2mm},\hspace{2mm} \alpha (1)=x_1\)
この\(\alpha \)を\(x_0\)から\(x_1\)への道とよぶ。\(\hspace{3mm}\alpha (0)\)を\(\alpha \)の始点、\(\alpha (1)\)を\(\alpha\)の終点とよぶ。
基本群の定義
基本群に欠かせないループを定義する.
\((X,\mathcal{O})\)を位相空間とする。
\(^{\forall}x_0 \in X\)について\(x_0\)から\(x_0\)への道を\(x_0\) を基点とするループとよぶ。
つまり始点も終点も一緒の道をループと呼ぶ.
実はこの元を全部集めた集合にちょこっと工夫をすると群になる.
\((X,\mathcal{O})\) を位相空間とする。
\(^{\forall}x_0 \in X\) について\(x_0\) の基本群\(\pi_1(X,x_0)\)とは
\(\pi_1(X,x_0):=\{ \alpha \mid \alpha はx_0 を基点とするループ\}/_{\simeq_p}\)のことである.
この定義を見ると,「基本群ってループを集めたものなのね.」とおおよそわかる.
しかしながらよくよく見ると\( \simeq_p\) という謎のマークがついているのがわかる.
これは道ホモトピーという同値関係だ.
難しいことは後回しにして今は
「連続変形できるものは同じものとみなしましょう」と思っていただいたら大丈夫である.
これでも分かりにくいと思うので解説する.
基本群の例
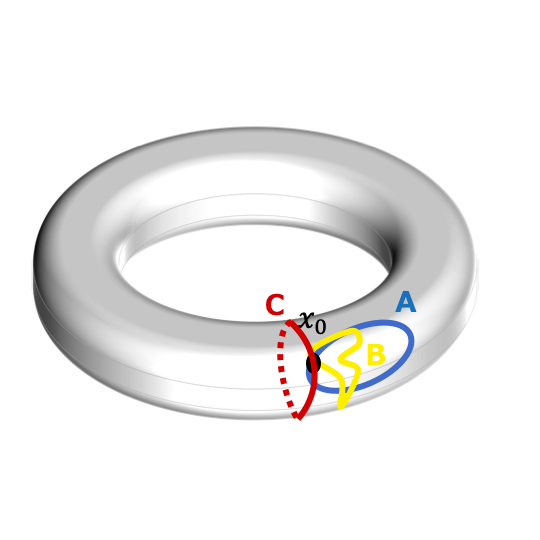
こんな風にドーナツの上にループを考える.
例えば \(A\) と \(B\) は別のループだが,
\(A\)のループをスルスルと手繰り寄せると\(B\) に変形することができる.
このように「連続変形できるものは同じものとみなしましょう」
というのが基本群の元でのルールだ.
ここで\(C\) について確認してみる.
すると,\(C\) をスルスルと手繰り寄せてもドーナツが引っかかって
\(A,B\)には連続変形できない.
このことから\(C\) は違う元として取り扱う.
終わりに
ここでは基本群の定義を直観的に説明した.
しかしながらまだ疑問はいくつか残る.
例えば「基本群はどうして群になるのか?」や「途中で出てきた道ホモトピーとは?」
「そもそもなんで基本群なんか考えるの?」など色々あげられる.
このことについては次回以降解説する.

コメント