外角定理(Exterior Angle Theorem)
三角形の任意の外角は、隣接しない内角のどれよりも大きい。
この主張は中立幾何の世界で可能となる。
三角形の定義は以前行った。(詳しくは中立幾何)
しかしここで主張にあがっている外角と隣接しない内角は新登場のため、
ここで定義する。
外角 隣接しない内角
\(\triangle ABC\)に対して、\(A-C-D\)となる点\(D\)をとる。
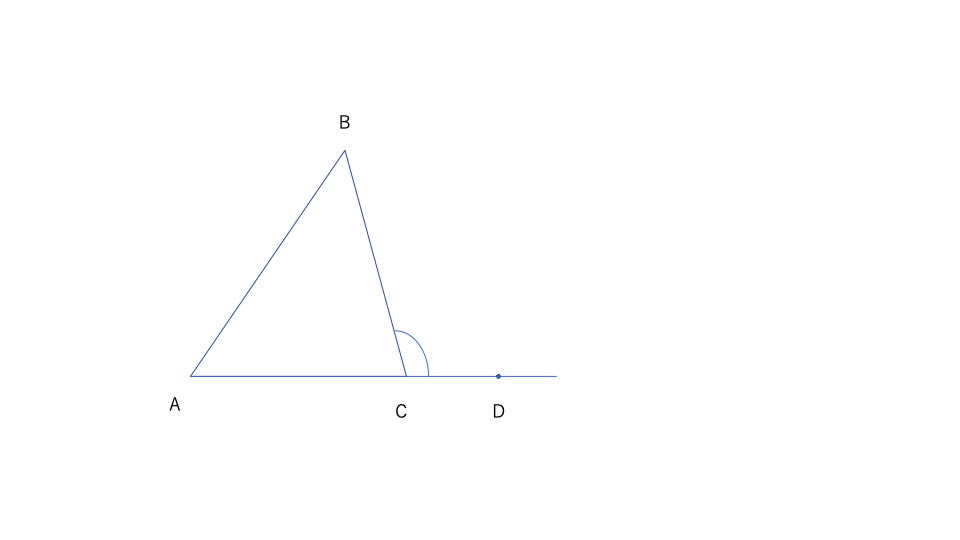
この時\(\angle BCD\)を\(\triangle ABC\)の頂点\(C\)での外角という。
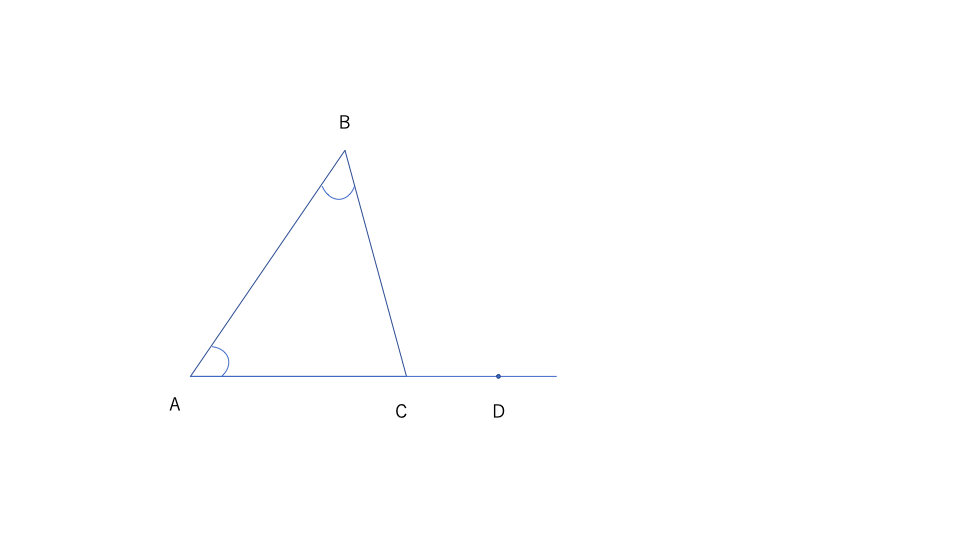
また外角\(\angle BCD\)に対して、\(\angle A\)と\(\angle B\)を隣接しない内角という。
図で表すと以下のようである。
\(A-C-D\)となる点\(D\)をとる。
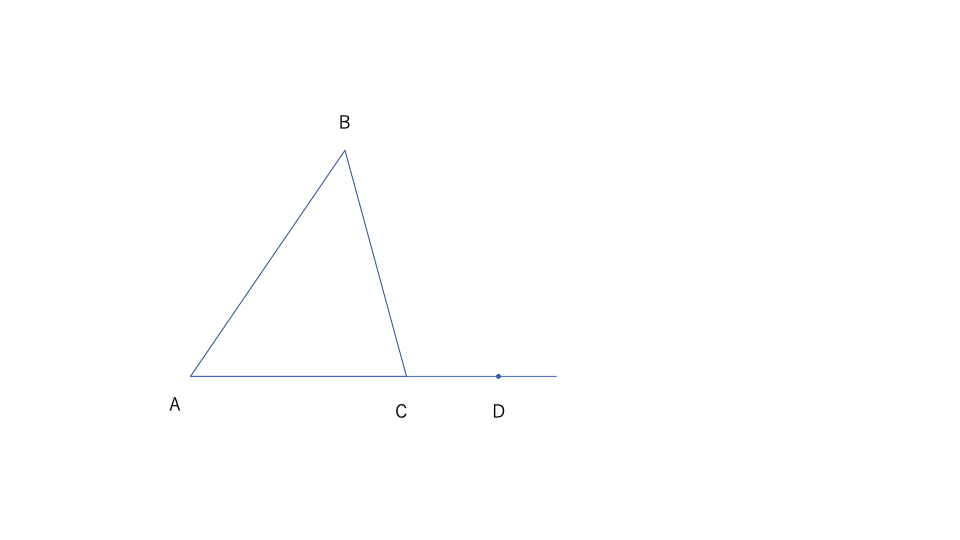
この時\(\angle BCD\)を\(\triangle ABC\)の頂点\(C\)での外角という。
また外角\(\angle BCD\)に対して、\(\angle A\)と\(\angle B\)を隣接しない内角という。
といった感じだ。
外角定理のロードマップ
直線角対の定義→LPT→角の合同の定義→対頂角対の定義→VPT→外角定理 の流れで証明する。
今はLPT、VPTって何やって感じに思っていただいて、順を追って理解していただければ嬉しい。
今回はこの直線角対までを解説する。
直線角対
2つの角\(\angle ABC\)と\(\angle CBD\)について、
\(A-B-D\)が成り立つ時、それら2つの角を直線角対とよぶ。
\(A,B,D\)という点が一直線上にあり、\(C\)という点がその直線上にない設定だ。
こんなイメージだ。
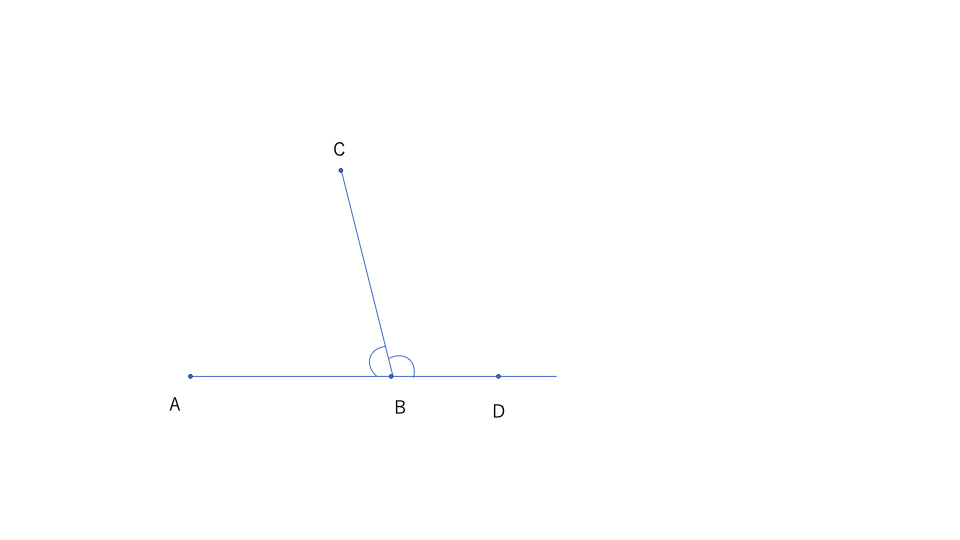
この定義には一見\(A,B,D\)が共線的と書いてあるだけで、\(C\)がこの直線上にないとはどこにも言及されていないように感じる。
ではこのことがなぜわかるかというと角の定義からである。
\(A,B,C\)を共線的でない3点とする。
\(\angle ABC=\overrightarrow{BA}\cup \overrightarrow{BC}\)を角\(ABC\)という。
また、このとき、点\(B\)を角\(\angle ABC\)の頂点という。
角を定義するときに、共線的でない3点で考えることをもう条件付けられているのだ。
そのことを踏まえてもう一度定義を見てみる。
2つの角\(\angle ABC\)と\(\angle CBD\)について、
\(A-B-D\)が成り立つ時、それら2つの角を直線角対とよぶ。
そうすると、\(A-B-D\)という条件があって\(\angle ABC\)という角を作っているなら、
\(A,B,D\)と\(C\)は同一直線上にあってはならないとわかる。
おまけ
直線角対を定義したあと何をするか先にネタバレすると次回はLPTという主張を証明する。
角\(\angle ABC,\angle CBD\)が直線角対を形成するならば、
\(m(\angle ABC)=m(\angle CBD)=180\)
この主張は分度器幾何の世界で可能となる。
これは小中高の感覚だと当たり前のように感じるかもしれないが、平面幾何的には偉大な事実だ。
なぜなら平面幾何では3点が共線的な場合、角を定めていない。
そのため、小中高の感覚で直線を測って「はい、角度は180」とはなる訳が無いのだ。
それにも関わらず直線角対の角度を足したら180となるのは驚くべきことなのだ。
このLPTを証明することの大切さを踏まえた上で分度器関数の定義をおさえておく。
パッシュ幾何\((\mathcal{P},\mathcal{L},d)\)における角全体の作る集合族を\(\mathcal{A}\)とする。
関数\(m:\mathcal{A}\rightarrow \mathbb{R}\)が次の3つの条件を満たすとき、分度器関数と呼ばれる。
\(1.\angle ABC \in \mathcal{A} \rightarrow 0<m(\angle ABC)<180\)\(2.\overrightarrow{BC}\)の定める半平面\(H\)を考える。
\(\hspace{5mm}\)このとき\(^{\forall}\theta \in (0,180) \hspace{3mm}^{\exists _1}\overrightarrow{BA}\hspace{2mm}s.t.\hspace{2mm}m(\angle ABC)=\theta\)
このとき、値\(m(\angle ABC)\)をその角の角度とよぶ。
1.角度は0より大きく180より小さいこと
2.指定した角度を実現する角を半平面上にただ一つだけ作れること
3.点\(D\)が\(\angle ABC\)の内部にあるとき、角度の足し算ができること
このことをおさえながら次回はLPTの証明ヘと迫る。



コメント