平面分割公理を満たす計量幾何をパッシュ幾何とよぶ。
計量幾何の定義は以下のようであった。(詳しくは計量幾何)
\((\mathcal{P},\mathcal{L},d)\)について以下の条件を満たすもの。
(1)\(^{\forall}l \in \mathcal{L}\)について目盛関数が存在すること。
計量幾何では、全ての直線に目盛がふってあるという事を要求している。
それに平面分割公理というものが追加されている。
平面分割公理
\( \hspace{10mm}(3)H_1,H_2\)は凸集合 \(\hspace{10mm}(4)A\in H_1,B\in H_2\Rightarrow \overline {AB}\cap l\neq \emptyset\)
この時、\(H_1,H_2\)を直線\(l\)の定める半平面とよぶ。
ざっくり言うと、「好きな直線を一本抜くと二つの世界に綺麗にパックリ割れる」という事だ。
このことを踏まえて、条件(1)~(4)をみていく。
条件(1)(2)
(1)では、平面から1本の直線を除いたら、2つの世界の和集合で表せることを要求して、
さらに(2)を加えることで、2つの世界にパックリ割れることを要求している。
条件(3)
\( (3)H_1,H_2\)は凸集合
平面の部分集合\(H\)が凸集合であるとは以下の条件を満たすこと。
\(^{\forall }A,B \in H\)について\(\overline{AB}\subset H\)
具体的に凸集合とは何だったかを図で確認すると、要求がわかる。
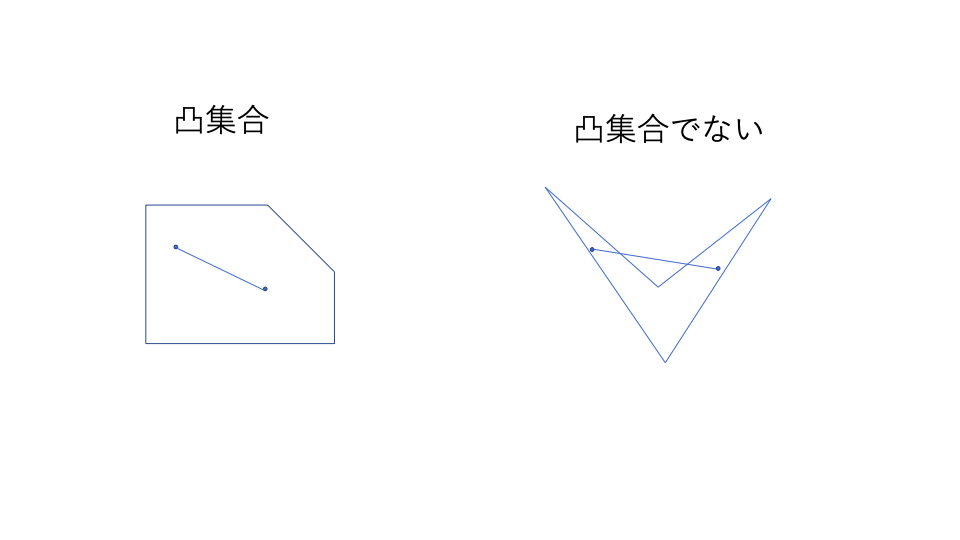
「好きに2点をとってきて、その線分を考えると、きっちり集合に含まれている。」ということ。
条件(4)
(4)A\in H_1,B\in H_2\Rightarrow \overline {AB}\cap l\neq \emptyset[/latex]
「Aの世界からBの世界に行くには、橋をかけなければならない。」ということを要求している。
参考文献
(1) 寺垣内 政一(2019) 『平面幾何の公理的構築』広島大学出版会
(2) Richard S.Millman and George D.Parker(1991)
『Geometry:A metric approach with models』Undergtaduate Texts in Mathematics



コメント