あらすじ
前回はハウスドルフ空間と連続について解説した。
(詳しくは、ハウスドルフ空間と連続,ハウスドルフ空間と連続(2))
今回はハウスドルフ空間と相対位相について見ていく。
おさらい
ハウスドルフ空間の定義は以下のようであった。(詳しくは、ハウスドルフ空間)
\((X,\mathcal{O})\)を位相空間とする。
\((X,\mathcal{O})\)がハウスドルフ空間であるとは以下の条件を満たすこと。
\(^{\forall}x_1,x_2 \in X (x_1 \neq x_2)\hspace{2mm} ^{\exists} O_1,O_2 \in \mathcal{O} \hspace{2mm}s.t.\hspace{2mm}x_1 \in O_1 ,x_2 \in O_2 ,\hspace{2mm}O_1 \cap O_2 = \emptyset\)ざっくり言うと、「異なる2点を持ってきたら交わらない開集合が取れる。」
また、相対位相の定義は以下のようであった。(詳しくは、相対位相)
\((X,\mathcal{O})\)を位相空間とし、部分集合\(A \subset X\)を考える。
この時、Aに\(\mathcal{O}_A=\{O \cap A| O \in \mathcal{O} \}\)という位相をいれる。
この時、\(\mathcal{O}_A\)を相対位相といい、\((A,\mathcal{O}_A)\)を\((X,\mathcal{O})\)の部分空間とよぶ。
ざっくり言うと「部分集合とそれぞれの開集合の交わりを位相とする。」ということ。
今回の主張
元々あった世界で成り立っている性質は局所的に見ても成り立っているような感覚はあると思う。
例えば、日本では日本語を話すという性質は東京でも大阪でも高知でもそうである。
(方言の違いはあるけれど。)
今回は元の世界\(X\)がハウスドルフ空間なら部分空間\(A\)でもハウスドルフ空間だと主張する。
\((X,\mathcal{O})\)を位相空間、部分空間\(A \subset X\)を考える。
この時、\((X,\mathcal{O})\)がハウスドルフ空間ならば、\((A,\mathcal{O}_A)\)もハウスドルフ空間。
今回の結論は\((A,\mathcal{O}_A)\)がハウスドルフ空間であること。
言い換えると、\(A\)から好きに2点持ってきて、上手いように交わらない開集合が取れることを示す。
だから証明の第一歩は、\(A\)から好きに2点持ってくることだ。
(証明)
\(^{\forall}a_1,a_2 \in A\)について考える。\(A \subset X\)より\(a_1,a_2 \in X\)
\((X,\mathcal{O})\)はハウスドルフ空間であるから\(^{\exists}O_1,O_2 \in \mathcal{O}\hspace{2mm}s.t.\hspace{2mm}a_1 \in O_1,a_2 \in O_2, O_1 \cap O_2 =\emptyset\)
さて、\(O_1 \cap O_2 =\emptyset\)より\(\hspace{2mm}(A \cap O_1) \cap(A \cap O_2) =\emptyset\)
相対位相の定義より\((A \cap O_1),(A \cap O_2) \in \mathcal{O}_A\)
まとめると、\(a_1 \in (A \cap O_1),a_2 \in (A\cap O_2) (A \cap O_1), \cap(A \cap O_2) =\emptyset\)
青い部分から\((A,\mathcal{O}_A)\)もハウスドルフ空間である。
証明解説
もう一度確認すると、今回の目的は「\(A\)がハウスドルフ空間であることを示す。」
すなわち\(A\)から好きに2点持ってきて、上手いように交わらない開集合が取れることを示すことだった。
しかし、\(A\)だけの世界ではどうしようもできない。
連続では、ハウスドルフ空間である\(Y\)に話を移して解決した。
今回は、ハウスドルフ空間である元の世界\(X\)に話を移して解決しようという戦法。
以下の証明のステップは図を持って解説する。
まず好きに2点とってくる。
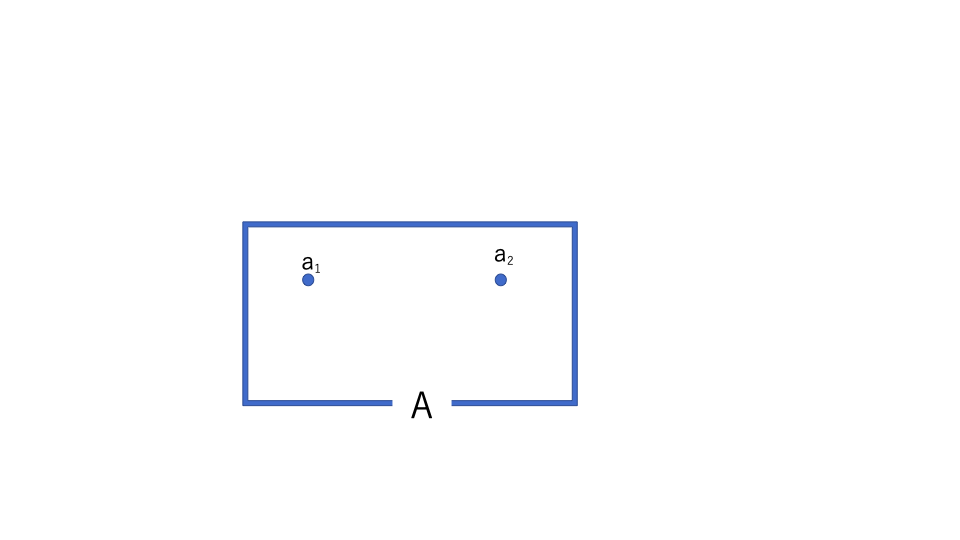
そして\(X\)に話を移す。
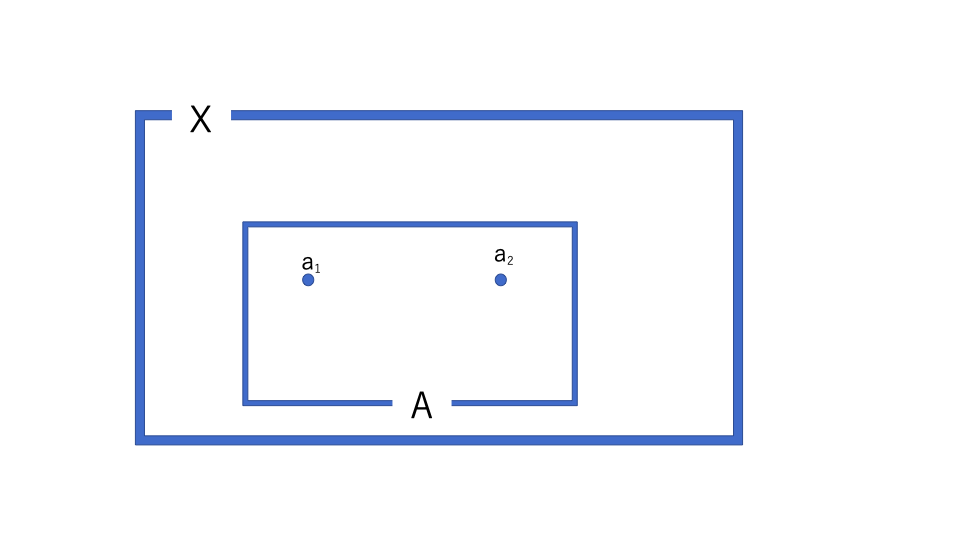
次に\(X\)がハウスドルフ空間であることを使って開集合をとる。
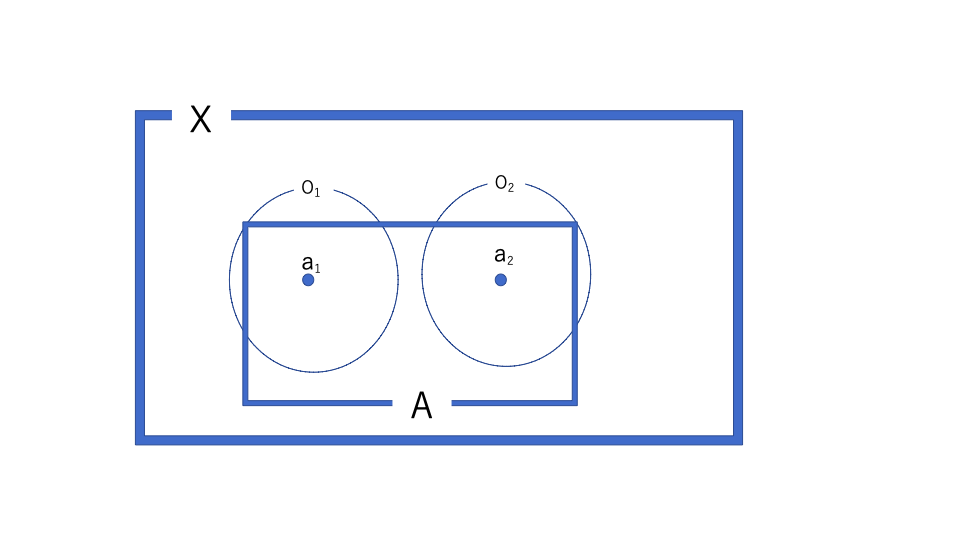
そして相対位相の定義から開集合と\(A\)の交わりを見る。
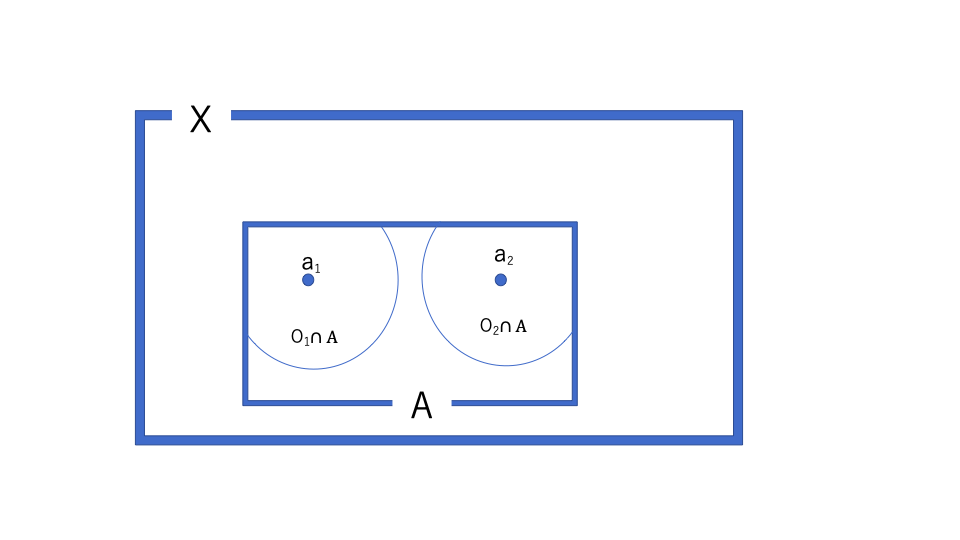
これにより証明することができた。



コメント