あらすじ
位相空間\((X,\mathcal{O}_X),(Y,\mathcal{O}_Y)\)と写像を考えて、\(f:X \rightarrow Y\)
行先の\((Y,\mathcal{O}_Y)\)がハウスドルフ空間であるとき、
\((X,\mathcal{O}_X)\)もハウスドルフ空間になるためにはどうしたら良いかを考えている。
前回は\(f:X \rightarrow Y\)に連続という条件をつけただけでは、
\((X,\mathcal{O}_X)\)にならないことを確認した。
(前回の内容はハウスドルフ空間と連続)
今回は連続という条件に何を加えると
「行先がハウスドルフならば、出発地もハウスドルフとなる」と言えるのかを考える。
前回から得たもの
前回の反例を再確認する。
\(X=\{あ,い,う\},\mathcal{O}_X=\{\emptyset ,X , \{あ,い\},\{う\}\}\)\((Y,\mathcal{O}_Y)\)を\(Y=\{A,B\},\mathcal{O}_Y\)を離散位相と定める。
また、\(f:X \rightarrow Y \)を\(f(あ)=f(い)=A,f(う)=B\)とする。
これは、「行先がハウスドルフならば、出発地もハウスドルフとなる」という祈願を
連続だけの条件では成し遂げられなかった例としてあげた。
しかし、実はこれはよく観察すると、他の条件を含んでいることがわかる。
それは、\(f\)の全射である。
今まで連続という条件だけでは、「行先がハウスドルフならば、出発地もハウスドルフとなる」
ということは成し遂げられなかったと言ってきたが、
実は全射で連続でも「行先がハウスドルフならば、出発地もハウスドルフとなる」は成し遂げられない。
では他に写像の条件を加えるとしたら何があるだろうかと考えると、単射が浮かぶ。
実は単射という条件があれば、目標を成し遂げることができる。
ハウスドルフと単射連続
位相空間\((X,\mathcal{O}_X),(Y,\mathcal{O}_Y)\)と写像\(f:X \rightarrow Y\)を考える。
\(f\)が単射連続で\((Y,\mathcal{O}_Y)\)がハウスドルフ空間ならば、
\((X,\mathcal{O}_X)\)もハウスドルフ空間である。
この証明はまずイメージしてもらいたい。
この証明の目標は「\((X,\mathcal{O}_X)\)もハウスドルフ空間であること」
すなわち「\(X\)から好きに2点とってきて、その2点を含むそれぞれが交わらない開集合を取れる」
さて、手順に沿って考える。
\(X\)から好きに2点\(x_1,x_2\)をとってくる。
ここで開集合を上手いようにとってきたいのだが、\(X\)内では残念ながらヒントがない。
だから次のように考える。
まず、\(y_1=f(x_1),y_2=f(x_2)\)を考えると、単射より\(y_1\neq y_2\)
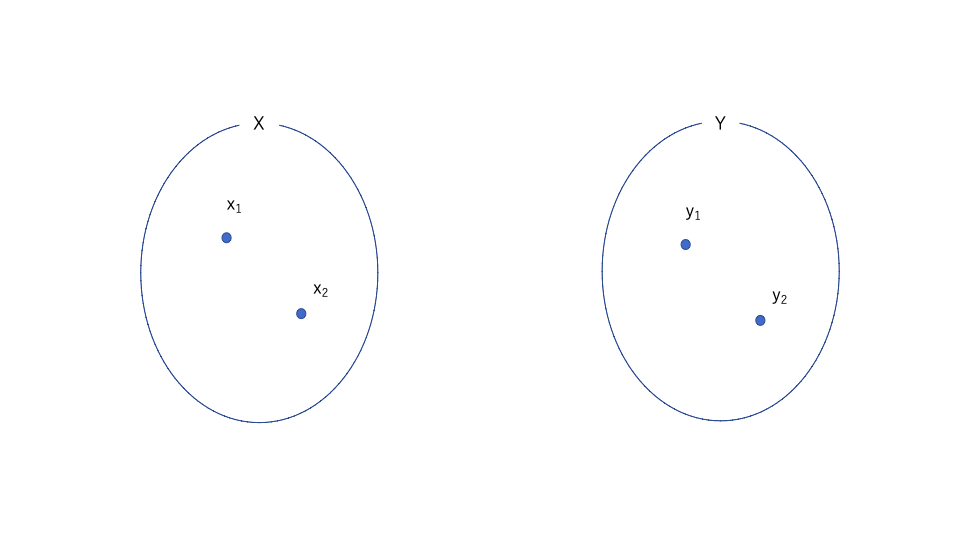
Yはハウスドルフ空間だから交わりのないグループを作ることができる。
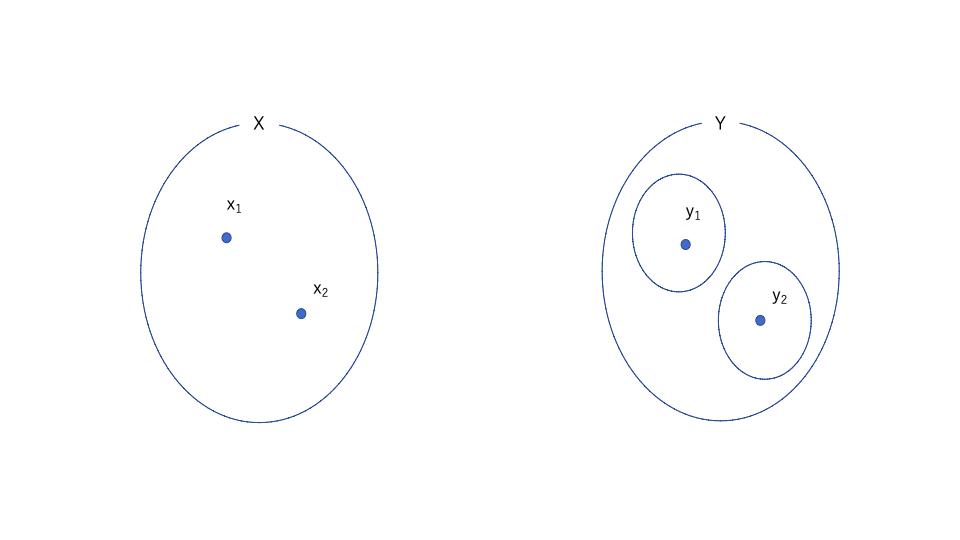
これのfの逆像を考えると、単射だから帰ってきても交わりがない。
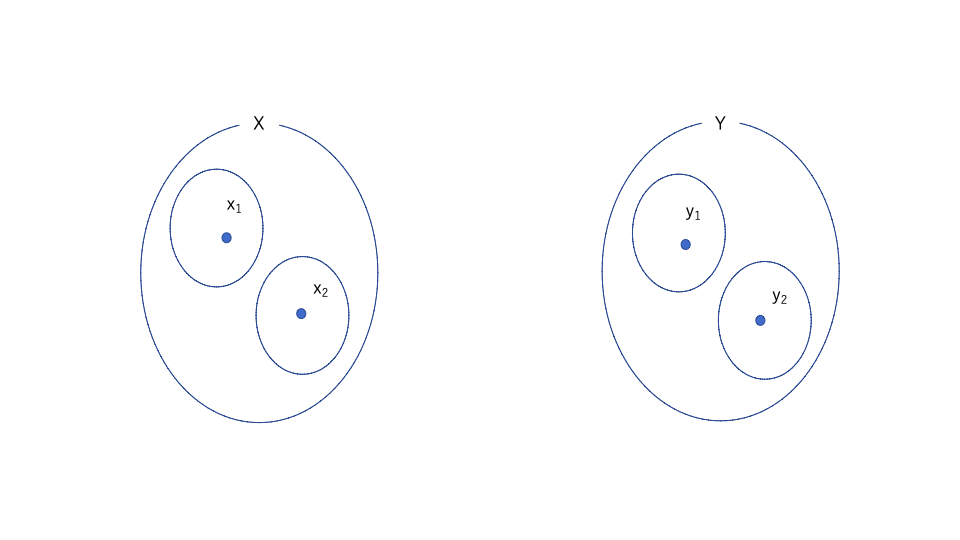
これより\((X,\mathcal{O}_X)\)はハウスドルフ空間と言える。
下には文章のみで証明をかく。
(証明)
\(^{\forall}x_1,x_2 \in X \hspace{2mm}(x_1 \neq x_2)\)について単射性より\(f(x_1) \neq f(x_2)\)
\(Y\)はハウスドルフ空間であるから、\(^{\exists}O_1,O_2 \in \mathcal{O}_Y\hspace{2mm}s.t.\hspace{2mm}f(x_1) \in O_1,f(x_2) \in O_2 ,O_1 \cap O_2 =\emptyset \)
\(f^{-1}(O_1),f^{-1}(O_2)\)は連続であるから\(X\)上で開集合。
この時、\(x_1 \in f^{-1}(O_1),x_2 \in f^{-1}(O_2)\)でまた、単射性より\(f^{-1}(O_1) \cap f^{-1}(O_2) = \emptyset \)
これより、\((X,\mathcal{O}_X)\)はハウスドルフ空間。



コメント