あらすじ
ハウスドルフ空間と積空間の関係を調べようと思った時に、3つほどアイデアが浮かぶ。
1つ目は「ハウスドルフ空間\((X,\mathcal{O}_X),(Y,\mathcal{O}_Y)\)の積空間\((X \times Y, \mathcal{O}_{XY})\)はハウスドルフ空間か。」
2つ目は「ハウスドルフ空間\((X,\mathcal{O}_X)\)とハウスドルフ空間でない\((Y,\mathcal{O}_Y)\)の積空間\((X \times Y, \mathcal{O}_{XY})\)はハウスドルフ空間か。」
3つ目は「\((X \times Y, \mathcal{O}_{XY})\)がハウスドルフ空間ならば\((X,\mathcal{O}_X),(Y,\mathcal{O}_Y)\)はハウスドルフ空間か。」
前回は1つ目が成り立っていたことを確認した。(詳しくはハウスドルフ空間と積空間)
今回は2つ目が成り立つのかどうかを考える。
おさらい
ハウスドルフ空間の定義は以下のようであった。(詳しくはハウスドルフ空間)
\((X,\mathcal{O})\)を位相空間とする。
\((X,\mathcal{O})\)がハウスドルフ空間であるとは以下の条件を満たすこと。
\(^{\forall}x_1,x_2 \in X (x_1 \neq x_2)\hspace{2mm} ^{\exists} O_1,O_2 \in \mathcal{O} \hspace{2mm}s.t.\hspace{2mm}x_1 \in O_1 ,x_2 \in O_2 ,\hspace{2mm}O_1 \cap O_2 = \emptyset\)ざっくり言うと「異なる2点をとると、上手いように交わらない開集合が取れる。」ということ。
また、積空間の定義は以下のようであった。(詳しくは積空間)
\((X,\mathcal{O}_X),(Y,\mathcal{O}_Y)\)を位相空間とする。
直積集合\(X \times Y\)に以下のように位相を定める。
\(\mathcal{B}=\{U \times V| U \in \mathcal{O}_X,V \in \mathcal{O}_Y\}\)を基底とし、これにより生成される位相を\(\mathcal{O}_{X\times Y}\)とする。
この時、\((X \times Y,\mathcal{O}_{X\times Y})\)を積空間、\(\mathcal{O}_{X\times Y}\)を積位相とよぶ。
ざっくり言うと「開と開の直積を開集合とし、それらを全部含めて基底とする。」ということ。
これを踏まえて、2番目の考察対象を見ていく。
2番目の考察
2つ目は「ハウスドルフ空間\((X,\mathcal{O}_X)\)とハウスドルフ空間でない\((Y,\mathcal{O}_Y)\)の積空間\((X \times Y, \mathcal{O}_{XY})\)はハウスドルフ空間か。」
条件を考える時は、反例になりそうなものをいくつか試して、成り立っていたら証明方法を考えるというのがセオリーである。
今回でいう反例になりそうなものとは
ハウスドルフ空間を考えるのに、ハウスドルフ空間でない方の位相を密着位相にすることだ。
そうして、以下のような場合を考えてみる。

このように、\(X\)からの要素の取り方を一緒にしてしまうと、
\(X\)が持つハウスドルフ性は発揮できない。
そして\((Y,\mathcal{O}_Y)\)には密着位相が入っているから、
\(X\)でどう頑張っても結局以下のようになる。
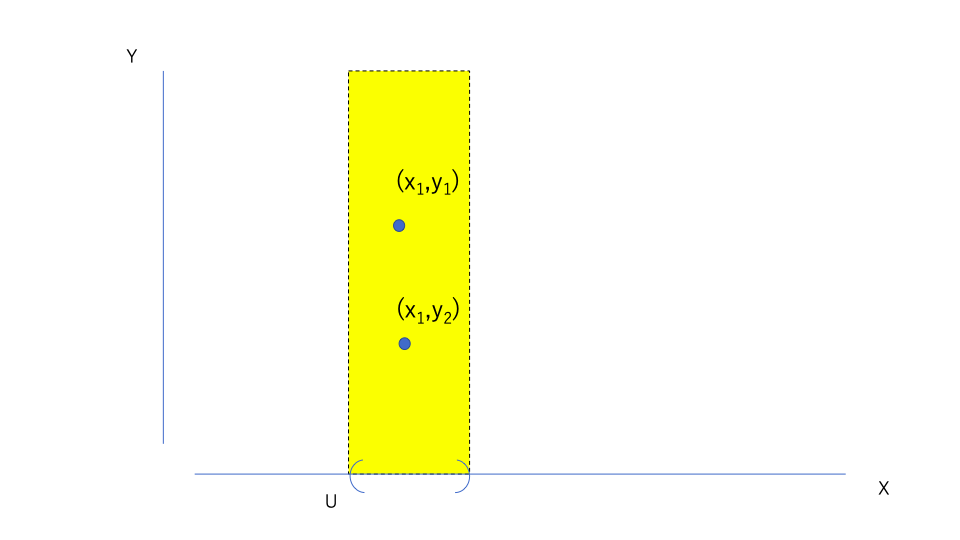
このように2点をとると、どう頑張っても一緒の開集合の中に入ってしまう。
これより(2)の条件では、ハウスドルフ空間になることができない。
おまけ
前回は(1)の条件、ざっくり言うと
「両方ハウスドルフなら積空間もハウスドルフ」は成り立つことを確認した。
今回は(2)の条件、ざっくり言うと
「片っぽハウスドルフ空間なら積空間もハウスドルフ」は成り立たないことを確認した。
次回は(3)の条件、ざっくり言うと
「積空間がハウスドルフなら元の空間はハウスドルフか」を考えていく。
\(\)


コメント