あらすじ
ハウスドルフ空間の定義は以下のようであった。
\((X,\mathcal{O})\)を位相空間とする。
\((X,\mathcal{O})\)がハウスドルフ空間であるとは以下の条件を満たすこと。
\(^{\forall}x_1,x_2 \in X (x_1 \neq x_2)\hspace{2mm} ^{\exists} O_1,O_2 \in \mathcal{O} \hspace{2mm}s.t.\hspace{2mm}x_1 \in O_1 ,x_2 \in O_2 ,\hspace{2mm}O_1 \cap O_2 = \emptyset\)ハウスドルフ空間の性質は他の概念にどのように維持されるのかを見てきた。
1回目はハウスドルフ空間と連続の関係を考察した。
(詳しくは、ハウスドルフ空間と連続,ハウスドルフ空間と連続(2))
2回目はハウスドルフ空間と部分空間の関係を考察した。
(詳しくは、ハウスドルフ空間と部分空間)
今回はハウスドルフ空間と積空間の関係を考察する。
今回の概要
積空間の定義は以下のようであった。(詳しくは積空間)
\((X,\mathcal{O}_X),(Y,\mathcal{O}_Y)\)を位相空間とする。
直積集合\(X \times Y\)に以下のように位相を定める。
\(\mathcal{B}=\{U \times V| U \in \mathcal{O}_X,V \in \mathcal{O}_Y\}\)を基底とし、これにより生成される位相を\(\mathcal{O}_{X\times Y}\)とする。
この時、\((X \times Y,\mathcal{O}_{X\times Y})\)を積空間、\(\mathcal{O}_{X\times Y}\)を積位相とよぶ。
この時の考察対象としては3つくらいが頭に浮かぶ。
1つ目は「ハウスドルフ空間\((X,\mathcal{O}_X),(Y,\mathcal{O}_Y)\)の積空間\((X \times Y, \mathcal{O}_{XY})\)はハウスドルフ空間か。」
2つ目は「ハウスドルフ空間\((X,\mathcal{O}_X)\)とハウスドルフ空間でない\((Y,\mathcal{O}_Y)\)の積空間\((X \times Y, \mathcal{O}_{XY})\)はハウスドルフ空間か。」
3つ目は「\((X \times Y, \mathcal{O}_{XY})\)がハウスドルフ空間ならば\((X,\mathcal{O}_X),(Y,\mathcal{O}_Y)\)はハウスドルフ空間か。」
今回からはこの3つについて考察していく。
(1)
「ハウスドルフ空間\((X,\mathcal{O}_X),(Y,\mathcal{O}_Y)\)の積空間\((X \times Y, \mathcal{O}_{XY})\)はハウスドルフ空間か。」
これが言えなかったら(2)も自動的に言えないということになる。
さて、積位相\((X \times Y, \mathcal{O}_{XY})\)がハウスドルフ空間かどうかを調べたいので、
最初にするべきことは\(X \times Y\)から好きに異なる2点をとってくることだ。

積位相だから、\((x_1,y_1) \neq (x_2,y_2)\)だが、\(x_1\neq x_2 \)かつ\(y_1\neq y_2 \)とは限らない。
上図のように\(y_1= y_2 \)となる可能性だってありうる。
しかしどちらかは確実に違うことは明らかなので、今回は\(x_1 \neq x_2\)として考える。
さて、\(x_1 \neq x_2\)であり、\((X,\mathcal{O}_X)\)はハウスドルフ空間であることから、
\(^{\exists}U,V \in \mathcal{O}_X \hspace{2mm}s.t.\hspace{2mm}x_1 \in U ,x_2\in V ,U\cap V =\emptyset\)この時、\(U\times Y,V\times Y\)をそれぞれ考えると以下のようになる。
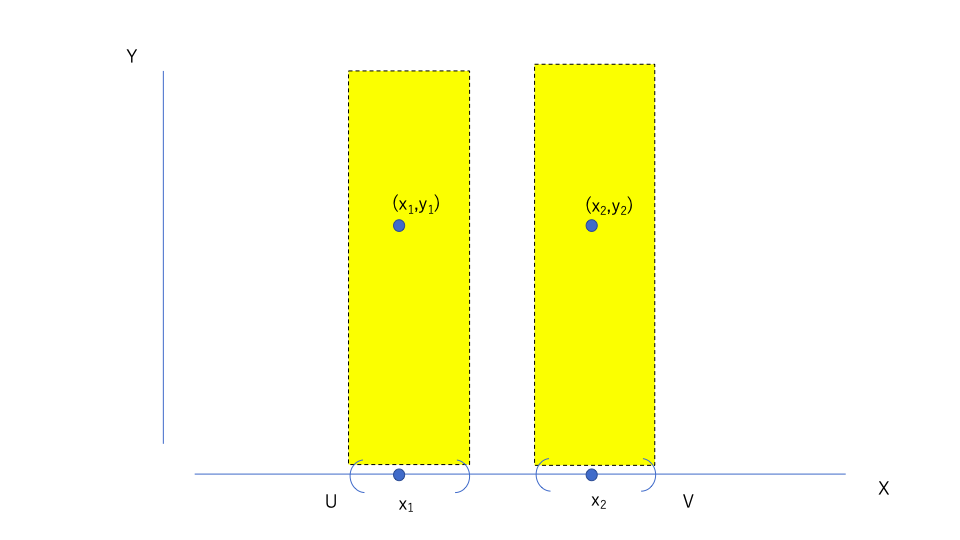
位相の定義から\(Y \in \mathcal{O}_Y\)なので、
\(U\times Y,V\times Y\)はそれぞれ積位相の基底であるから、積空間の開集合。
上手いように交わらない開集合をとることができたので、積空間もハウスドルフ空間となる。
おまけ
今回は(1)を考察した。次回は(2)を考察していく。



コメント