あらすじ
位相空間は考察対象がゆるゆるのため、様々な制限の設け方があるのだが、
その制限の設け方の中でも「分離公理」と呼ばれる有名なものがある。
その分離公理でも一番有名なのがハウスドルフ空間(\(T_2\)空間)である。
この制限を設けることで位相空間レベルではできなかった性質の話ができるようになる。
(実数ではできないが、自然数だと素因数分解の一意性の性質の話ができる的な。)
今回は、このハウスドルフ空間(\(T_2\)空間)とはどのような定義なのかを見ていく。
定義
ハウスドルフ空間
\((X,\mathcal{O})\)を位相空間とする。
\((X,\mathcal{O})\)がハウスドルフ空間であるとは以下の条件を満たすこと。
\(^{\forall}x_1,x_2 \in X (x_1 \neq x_2)\hspace{2mm} ^{\exists} O_1,O_2 \in \mathcal{O} \hspace{2mm}s.t.\hspace{2mm}x_1 \in O_1 ,x_2 \in O_2 ,\hspace{2mm}O_1 \cap O_2 = \emptyset\)定義解説
\(^{\forall}x_1,x_2 \in X (x_1 \neq x_2) \hspace{2mm} ^{\exists} O_1,O_2 \in \mathcal{O} \hspace{2mm}s.t.\hspace{2mm}x_1 \in O_1 ,x_2 \in O_2 ,\hspace{2mm}O_1 \cap O_2 = \emptyset\)
これは次のような工程を表している。
「まず、集合\(X\)から好きに異なる2点\(x_1,x_2\)をとってくる。
それぞれの点を含む開集合\(O_1,O_2\)を上手いように持ってくると、その開集合同士が交わりがない」
ということだ。
今回の内容はベン図で書くとイメージしやすくなる。
まず、集合\(X\)から好きに2点\(x_1,x_2\)をとってくる。
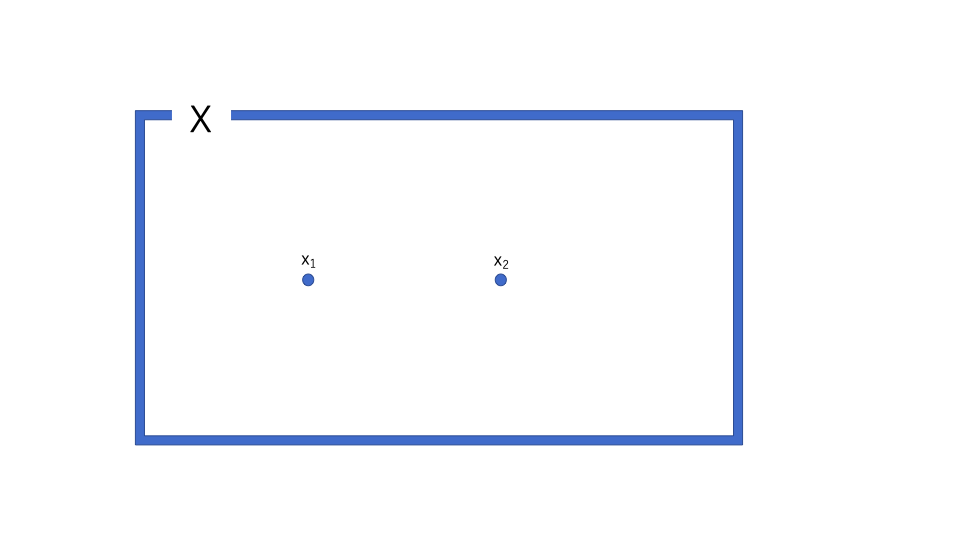
それぞれの点を含む開集合\(O_1,O_2\)を上手いように持ってくると、その開集合同士が交わりがない
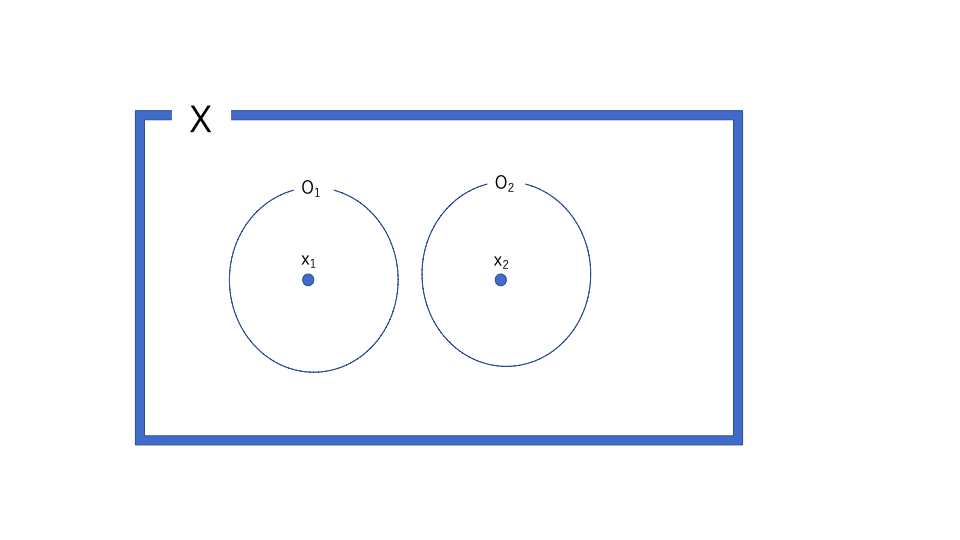
みたいな感じだ。
「クラスで2人が喧嘩しても、その2人が関わらないグループが作れる。」くらいのニュアンスだ。
(1点集合が開集合と定められているならば、そのグループは1人ぼっちかもしれないが…。)



コメント