粗幾何学とは何か？

はじめに

「数学とは異なったものを同じと見なす技術である 」

数学者アンリ・ポアンカレはこんな名言を残していたそうだ．

確かに，犬のポチとムギとレオのことと，子供と父親と母親の家族構成のことを同じ「3」として見ることは数学ならではの発想なのかもしれない．

　粗幾何学も同様にある見方を通して異なるものを同じものとみなす学問だ．

位相空間は\( \mathbb{R}\) と\((0,1)\) を同一視した．ざっくりいうと伸び縮みできるゴムみたいな幾何学だ．

それに対し，粗幾何学では\(\mathbb{R}\) と\(\mathbb{Z}\) を同一視する．ざっくりいうと薄目で見るような粗っぽい数学だ．

位相空間も粗幾何学も距離空間を一般化した概念だが，別の部分を抽象化している．

今回の記事では，粗幾何学の定義を見ていく．

粗空間の定義

位相空間では点や集合を好きに取ってきて，そこから近傍を考えましょうという考え方があった．

しかし距離空間に戻ってみると先に半径\(r>0\) を決めて，そこから任意の点や集合に対して\(r\)近傍を定めることができる．

つまり「点や集合を選ぶ→近傍を考える．」ではなく，
「近傍の作り方を考える→点や集合を好きに選ぶ→近傍が手に入る」みたいな道筋がある．

この考え方を抽象化したのが粗空間だ．

粗空間ではまずcontrolled setと呼ばれる\(E\subset X\times X\) を考える．

\(E\subset X\times X\) を考えると次の図のように任意の集合\(S\) に対して，\(E\) 近傍\(E[S]\) を考えることができる．

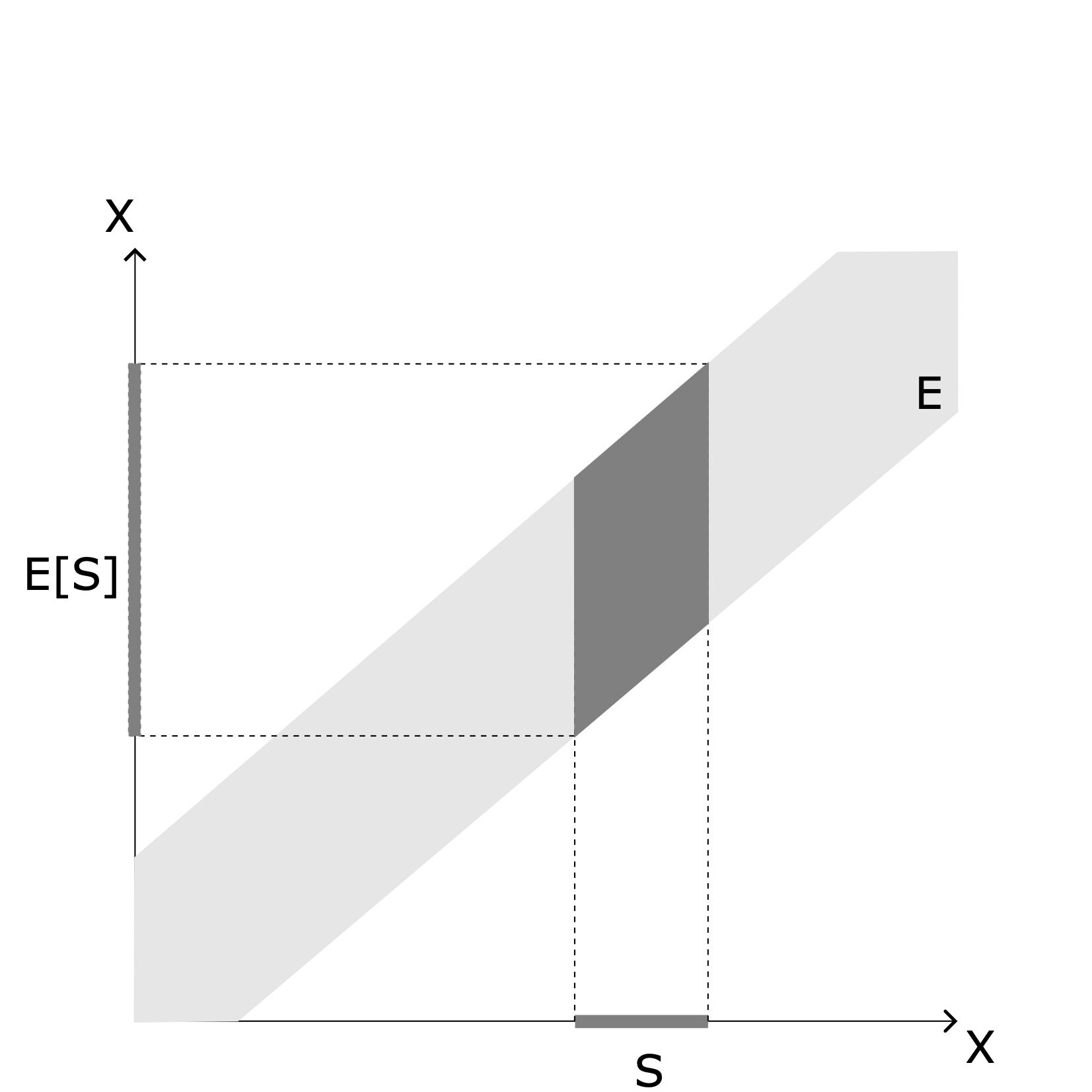
この図を意識しながら粗幾何学の定義をする．

1,2,4,5は近傍の言葉で改めて書くことができる．(3は私はまだ掴みきれていない)

1.\(\Delta :=\{ (x,x)\mid x\in X\} \in \mathcal{E}\)

1は何もふくらまさない，集合をそのまま返す近傍がありますよ，と言っている．

2.\(E\in \mathcal{E}\) ならば任意の\(E’\subset E\) に対して \(E’\in \mathcal{E}\)

2は\(E\) 近傍よりも小さくする近傍はいくらでも調整が効きますよ，と言っている．

4.\(E_1,E_2\in \mathcal{E}\) ならば
\(E_1\circ E_2:=\{(x,z)\mid \exists y\in X \mathrm{s.t.} (x,y)\in E_1,(y,z)\in E_2\}\in \mathcal{E}\)

4は\(E_1\) 近傍を取って\(E_2\) 近傍をとることは\(\mathcal{E}\) 内でできますよ，と言っている．

5.各\(i=1,\cdots ,n\) に対して\(E_i\in \mathcal{E}\) ならば ，\(\cup_{i=1}^nE_i \in \mathcal{E}\)

5は近傍の有限和くらいだったら\(\mathcal{E}\) 内でできますよ，と言っている．

こんなふうに粗幾何学は一様的な近傍を距離空間から一般化したものだ．

終わりに

今回は粗幾何学の概念をざっくりと紹介しながら粗空間を定義した．

次回は粗空間の例を見ていく．

参考文献

 John Roe, Lectures on Coarse Geometry, University LECTURE Series Volume 31, American Math- ematical Society