ハウスドルフ空間と積空間　最終回

あらすじ

ハウスドルフ空間はそれぞれの概念にどう引き継がれているのかを確認した。

最初はハウスドルフ空間と連続の関係について考察した。
(詳しくはハウスドルフ空間と連続)

次にハウスドルフ空間と部分空間の関係について考察した。
(詳しくはハウスドルフ空間と部分空間)

そして、ハウスドルフ空間と積空間については3つの考察対象を考えた。

1つ目は「ハウスドルフ空間\((X,\mathcal{O}_X),(Y,\mathcal{O}_Y)\)の積空間\((X \times Y, \mathcal{O}_{XY})\)はハウスドルフ空間か。」
(詳しくはハウスドルフ空間と積空間)

2つ目は「ハウスドルフ空間\((X,\mathcal{O}_X)\)とハウスドルフ空間でない\((Y,\mathcal{O}_Y)\)の積空間\((X \times Y, \mathcal{O}_{XY})\)はハウスドルフ空間か。」
(詳しくはハウスドルフ空間と積空間(2))

3つ目は「\((X \times Y, \mathcal{O}_{XY})\)がハウスドルフ空間ならば\((X,\mathcal{O}_X),(Y,\mathcal{O}_Y)\)はハウスドルフ空間か。」

今回はこの3つ目を考える。

3つ目の考察

本来は\((X,\mathcal{O}_X),(Y,\mathcal{O}_Y)\)どちらも確認しなければならないが、どちらも議論は同じなので、
\((X,\mathcal{O}_X)\)がハウスドルフ空間であることが確認できたらOK.

\((X,\mathcal{O}_X)\)がハウスドルフ空間だと示したいので、1手目は\(X\)から好きに2点取ってくることだ。

\(^{\forall}x_1x_2 \in X \)について上手いように交わらない開集合が取れたらOK.

さて、\(X\)で話を進めてもどうしようもないので、ハウスドルフ空間である積空間に話を移す。

\(Y\)の要素を揃えて、2点\((x_1,y_1),(x_2,y_1)\)を考える。

ハウスドルフ空間だから、\((x_1,y_1),(x_2,y_1)\)について上手いように2つの開集合\(O_1,O_2\)が取れる。

この時次の性質を満たす。\((x_1,y_1) \in O_1,(x_2,y_1) \in O_2 ,O_1 \cap O_2 =\emptyset \)

積空間におけるハウスドルフ空間

しかし、\(O_1,O_2\)が開集合\(U,V\)の\(U \times V\)型しているとは限らない。

なぜなら、\(U \times V\)型は位相ではなく基底なので、\(U \times V\)とは限らない。

しかし基底ではあるので、\(O_1=\cup_{\lambda \in \Lambda}(U_\lambda \times V_\lambda) ,O_2=\cup_{\lambda  ′ \in \Lambda  ′}(U_\lambda  ′ \times V_\lambda  ′)\)とかける。

この\(O_1=\cup_{\lambda \in \Lambda}(U_\lambda \times V_\lambda)\)の中で、ある\((U_a \times V_a )\)が\((x_1,y_1)\)の点を含んでいる。

同様に\(O_2=\cup_{\lambda  ′ \in \Lambda  ′}(U_\lambda  ′ \times V_\lambda  ′)\)の中でも、ある\((U_a ′ \times V_a ′)\)が\((x_2,y_1)\)の点を含んでいる。

和集合に入っているということは、誰かが要素を持っているという話である。
「ジャニーズに釣り好きがいるなら嵐か、Snow Manか、どこかのグループには釣り好きがいる」といっても良いといったらしっくりくるだろう。

結果的に\((x_1,y_1),(x_2,y_1)\)を含む\((U_\lambda \times V_\lambda),(U_\lambda  ′ \times V_\lambda  ′)\)型の交わらない開集合が見つかった。

説明のまとめ

さて、今までのことをおさらいする。

1手目は\(X\)から好きに2点取ってくる。

2手目は積空間に話を持ち込んで、ハウスドルフ空間である性質を用いながら
\((x_1,y_1),(x_2,y_1)\)を含む\((U_\lambda \times V_\lambda),(U_\lambda  ′ \times V_\lambda  ′)\)型の交わらない開集合が見つかった。

図にまとめると以下のようになる。

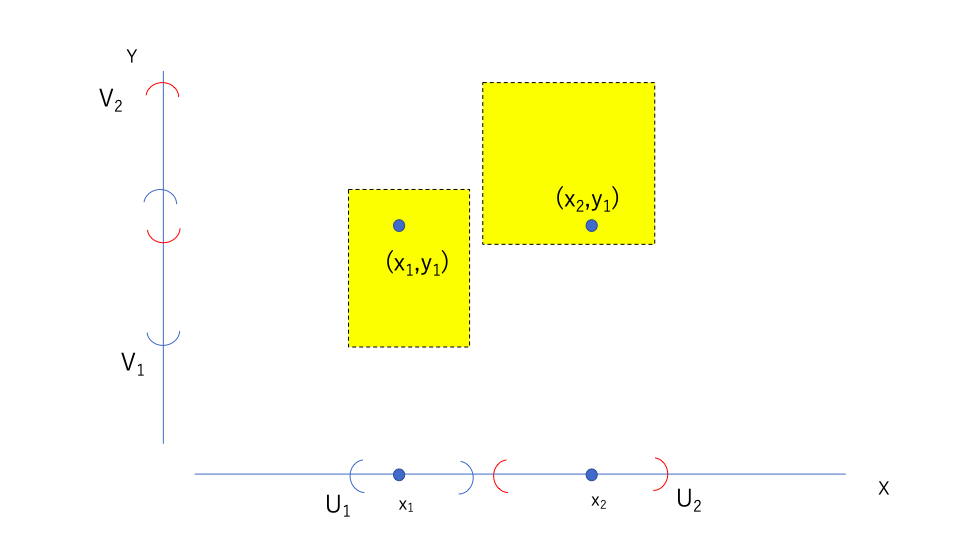
このように\(U_1 \cap U_2 =\emptyset \)となるしか他ない。

もし、\(U_1 \cap U_2 \neq \emptyset\)とすると、\(x_3 \in U_1 \cap U_2\)という点が見つかる。

この時、\((x_3,y_1)\)を考えると、どんな\(V_1,V_2\)でもy座標が揃ってるから、
\((x_3,y_1) \in U_1 \times V_1\)かつ\((x_3,y_1) \in U_2 \times V_2\)だからハウスドルフであることに反してしまう。

よって\(U_1 \cap U_2 =\emptyset \)となる。

したがって、\((X,\mathcal{O}_X)\)がハウスドルフ空間である。

\(\)